Résolution d'une équation avec paramètre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juil 2009, 14:12
par Dinozzo13 » 29 Juil 2009, 14:12
j'ai trouvé que x'>0 et x''<0
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 29 Juil 2009, 14:16
par Djmaxgamer » 29 Juil 2009, 14:16
Une derniere chose, tu dois prouver que x'0, on a 00[/TEX] :
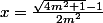
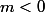
:
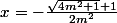
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juil 2009, 14:20
par Dinozzo13 » 29 Juil 2009, 14:20
Ok, d'accord j'ai compris. Y a-t-il autre chose à dire ou est-ce que c'est fini ?
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 29 Juil 2009, 14:29
par Djmaxgamer » 29 Juil 2009, 14:29
non si tu as compris c'est bon...
Essaye de résoudre :
=\ln(\sqrt{5-2x}))
Je viens de le faire j'ai la solution, on pourra vérifier =D
ps : elle est un peu plus simple vu qu'il n'y a qu'une seule possibilité pour m à vérifier.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 29 Juil 2009, 14:40
par Dinozzo13 » 29 Juil 2009, 14:40
Là tout de suite je n'ai pas le temps, je te posterais mon résultat ce soir :briques: :marteau: :ptdr:
-
p052
- Membre Naturel
- Messages: 17
- Enregistré le: 21 Juil 2009, 20:18
-
 par p052 » 29 Juil 2009, 15:35
par p052 » 29 Juil 2009, 15:35
Salut
Aprés résolution, je trouve :
S= {(-1+racine de (1+80m^4))/16m^4
Avec cette solution comprise entre 0 et 5/2 quel que soit m appartenant à R (étoile).
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 29 Juil 2009, 15:38
par egan » 29 Juil 2009, 15:38
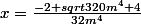
pour tout m différent de 0.
C'est ça ?
C'est marrant comme jeu en tout cas. ^^
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 29 Juil 2009, 15:43
par Djmaxgamer » 29 Juil 2009, 15:43
Déjà egan "pour tout m différent de zéro" est faux, le logarithme népérien n'est pas défini pour m négatif !
De plus la solution est fausse... EDIT : non ça revient au même tu as juste, faut juste faire attention au domaine de définition.
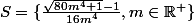
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 29 Juil 2009, 15:46
par egan » 29 Juil 2009, 15:46
Flûte, je me suis planté dans mes calculs. :marteau:
-
p052
- Membre Naturel
- Messages: 17
- Enregistré le: 21 Juil 2009, 20:18
-
 par p052 » 29 Juil 2009, 15:47
par p052 » 29 Juil 2009, 15:47
m peut être négatif car il est élevé au carré dans le logarithme népérien mais la soltution est effectivement fausse...
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 29 Juil 2009, 15:47
par egan » 29 Juil 2009, 15:47
Djmaxgamer a écrit:Déjà egan "pour tout m différent de zéro" est faux, le logarithme népérien n'est pas défini pour m négatif !
De plus la solution est fausse... EDIT : non ça revient au même tu as juste, faut juste faire attention au domaine de définition.
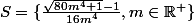
Mais m² est toujours positif.
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 29 Juil 2009, 15:48
par Djmaxgamer » 29 Juil 2009, 15:48
p052 a écrit:m peut être négatif car il est élevé au carré dans le logarithme népérien mais la soltution est effectivement fausse...
Oui tu as raison petit plantage de mémoire...
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 29 Juil 2009, 15:49
par Djmaxgamer » 29 Juil 2009, 15:49
egan a écrit:Flûte, je me suis planté dans mes calculs. :marteau:
nope c'est bon en fait =D
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 29 Juil 2009, 20:19
par egan » 29 Juil 2009, 20:19
Une autre. ^^
J'ai pas essayé encore mais elle a une tête qui me déplaît pas. :ptdr:
=ln(\frac{1}{\sqrt[3]{3x-2}}))
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 29 Juil 2009, 20:37
par Euler911 » 29 Juil 2009, 20:37
Bonsoir,
Bonne chance à celui qui trouvera la solution de ton équation egan ... C'est toi qui l'a inventée?
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 29 Juil 2009, 20:42
par egan » 29 Juil 2009, 20:42
Oui j'ai fait ça au pif. Ca me parraissait joli. Je cherche tout doucement là.
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 29 Juil 2009, 20:55
par egan » 29 Juil 2009, 20:55
La seule grosse grosse difficulté ce sont les grosses équations polynomiales sur lesquelles on tombe à la fin (7ème degrès si je ne me suis pas tromper).
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 29 Juil 2009, 21:04
par Euler911 » 29 Juil 2009, 21:04
C'est bien là le problème... vas-y pour résoudre ton équation de degré 7!!!!!!!! A part chercher par tâtonnement une solution... ça va être dur!
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 29 Juil 2009, 22:42
par xyz1975 » 29 Juil 2009, 22:42
Djmaxgamer a écrit:Ensuite tu peux conclure :
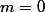
: pas de solutions
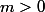
:
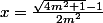
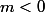
:
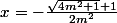
Il est faut d'envisager le cas m=0.
-
Djmaxgamer
- Membre Relatif
- Messages: 337
- Enregistré le: 27 Juin 2009, 12:43
-
 par Djmaxgamer » 30 Juil 2009, 01:15
par Djmaxgamer » 30 Juil 2009, 01:15
xyz1975 a écrit:Il est faut d'envisager le cas m=0.
Donc c'est soit dit dans l'énoncé (...pour m different de 0...) ou alors on doit le préciser nous même...c'est ça ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
