Nombre complexe Ts
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 18 Sep 2013, 21:25
par sosmath16 » 18 Sep 2013, 21:25
Bonjours a tous , voila alors j'écris à propos d'un devoir que je dois faire et qui traite sur les nombre complexes que je viens de commencer et je suis malheureusement déja perdue :( et le fait d'avoir un très mauvais prof l'année dernière n'arrange rien bref voila le sujet :
On considère le polynôme P tel que : P(z)=z^3-(6-4i)z²+(34-24i)z+136 i ou z est une variable complexe.
Exercice 1 :
1. Démontrer que P(z) possède une racine imaginaire pure.
2. Factoriser alors P(z).En déduire toutes les racines de P(z).
3. Placer dans le plan complexe muni d'un repère orthonormal les points-images des racines de P(z).
Quelle est la nature de la figure obtenue?
Exercice 2 :
Le plan complexe est rapporté à un repère orthonormal (O,u,v)
On considère les trois points: M d'affixe z (un complexe quelconque), M' d'affixe z² et M'' d'affixe z^3.
Quel est l'ensemble des points M tels que MM'M'' soit un triangle équilatéral?
Voila merci d'avance pr votre aide :jap:
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 18 Sep 2013, 21:43
par XENSECP » 18 Sep 2013, 21:43
Ex1 1) Et oui 4i est une racine de P(z).
Pour le trouver tu prends
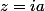
avec a réel.
Tu remplaces et tu mets la partie imaginaire de côté. Dans la partie réelle restante tu verras que seul a = 0 ou a = 4 et il se trouve que quand tu remplaces a par 4 dans la partie imaginaire tu obtiens bien 0.
0 + 0 = CQFD
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 18 Sep 2013, 21:54
par sosmath16 » 18 Sep 2013, 21:54
Daccord je comprends à peu près mais par contre , pourquoi z=ia ? Je pensais que cétait z=a+ib
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 18 Sep 2013, 23:36
par XENSECP » 18 Sep 2013, 23:36
Dans le cas général oui mais là tu essayes de prouver qu'un imaginaire pur est racine... Donc tu poses ia (imaginaire pur) et tu vérifies que tu trouves une valeur de a tel que c'est vrai (racine de P).
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 07:39
par sosmath16 » 19 Sep 2013, 07:39
Ah ok ! Je comprends :D du coup pr la 2eme question je vais devoir poser l'opération en remplaçant a soit par 0, soit par 4 ? Mais le fait qu'il soit remplaçable par ces 2 chiffres ne répond-il pas à la question 2 directement ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 19 Sep 2013, 07:42
par XENSECP » 19 Sep 2013, 07:42
Tu factorise par i a et tu as ensuite un polynôme de degré 2 (complexe certes) dont tu sais trouver les racines ;)
D'ailleurs il est évident que 0 n'est pas racine. Fais les calculs tu verras bien.
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 17:09
par sosmath16 » 19 Sep 2013, 17:09
Re , j'ai essaye de faire le calcul mais j'ai l'impression de me planter un peu d'aide ? :{
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Sep 2013, 17:50
par Sylviel » 19 Sep 2013, 17:50
La réponse de XENSECP a été un peu laconique. En fait tu factorise ton polynome par
(z - racine) donc ici par (z - 4i) (à toi de trouver l'autre polynome).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 18:39
par sosmath16 » 19 Sep 2013, 18:39
Merci pr cette 2eme explication mais je bug dès la 1ere question j'ai vrmt du mal :(
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 18:52
par sosmath16 » 19 Sep 2013, 18:52
Pour être précis je n'arrive pas à faire la démarche du calcul dois-je remplacé tt les z par a+ib ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 19 Sep 2013, 19:16
par XENSECP » 19 Sep 2013, 19:16
sosmath16 a écrit:Pour être précis je n'arrive pas à faire la démarche du calcul dois-je remplacé tt les z par a+ib ?
Dans quelle question?
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 19:25
par sosmath16 » 19 Sep 2013, 19:25
Le petit 1 :(
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 19 Sep 2013, 19:27
par XENSECP » 19 Sep 2013, 19:27
sosmath16 a écrit:Le petit 1

Tu le fais exprès ?
Tu remplaces z par ia !!!!!!!!
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 19:35
par sosmath16 » 19 Sep 2013, 19:35
c'est ce que j'ai fais ça m'a donné : (ia)^3-(6-4i)(ia)^2+(34-24i)ia+136i , dnc j'ai bien compris qu'il faut séparer réel et imaginaire mais je n'y arrive pas et ne tombe pas sur 4i :/
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 19 Sep 2013, 19:42
par XENSECP » 19 Sep 2013, 19:42
Fais le et on rediscute. En tout cas c'est clair que tu vas pas "tomber" sur 4i.
Tu vas isoler les parties réelles et partie imaginaires et dire que chacune doit être égale à 0 ou sinon "ia" n'est pas racine.
-
Afonso
- Messages: 6
- Enregistré le: 19 Sep 2013, 19:08
-
 par Afonso » 19 Sep 2013, 19:54
par Afonso » 19 Sep 2013, 19:54
Après tu développe ce que t'a trouvé et t'es censé trouver
-a^3i - (-6a^2+4a^2i) + 34ai + 24a + 136i
après tu met ceux qui on que (a) d'un côté et tu met ceux qui on i de l'autre en mettant i en facteur
PS : C'est vrai que J.Dou...c 1S2 c'était pas terrible
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 20:24
par sosmath16 » 19 Sep 2013, 20:24
@Afonso merci pr ta réponse :) il y'a juste que je ne comprends pas comment tu tombe sur -a^3i ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 19 Sep 2013, 20:26
par XENSECP » 19 Sep 2013, 20:26
-ia^3 pour être plus clair.
-
Afonso
- Messages: 6
- Enregistré le: 19 Sep 2013, 19:08
-
 par Afonso » 19 Sep 2013, 20:29
par Afonso » 19 Sep 2013, 20:29
sosmath16 a écrit:@Afonso merci pr ta réponse

il y'a juste que je ne comprends pas comment tu tombe sur -a^3i ?
i^3 = -i
donc (ai)^3 = a^3 * i^3 = a^3 * -i = -a^3i
-
sosmath16
- Membre Naturel
- Messages: 12
- Enregistré le: 12 Sep 2013, 17:56
-
 par sosmath16 » 19 Sep 2013, 20:37
par sosmath16 » 19 Sep 2013, 20:37
Daccord merci je suis bien tombé sur le bon résultat ( j'ai du faire un système) :D merci pr cette question ! Je passe à la 2 ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
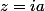 avec a réel.
avec a réel.