Réels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 14:23
par pluie2 » 15 Sep 2013, 14:23
Bonjour, j'aimerais avoir une aide sur cet exo de sup :
Soit x>0 et soit u la suite définie par : pour tout n appartient aux entiers naturels, u(n)=(x^n)/n!.
a) Déterminer le plus petit N des entiers naturels tel que u(n+1)/u(n) < 0.5
b) Montrer alors que pour tout n appartenant aux entiers naturels tel que n;)N, on a 0
j'ai fait :
a) u(n+1)/u(n) < 0.5 = (x^(n+1))/(n+1)! * n!/x^n = x/(n+1) < 0.5 = n < 2x-1.
et le reste je n'y arrive pas.
merci de me dnner des pistes :help:
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 15:01
par Anneauprincipal » 15 Sep 2013, 15:01
Bonjour,
Pour la première attention au changement d'inégalité quand tu passes à l'inverse.
Si

, alors

, et aussi
^2$)
etc... Il faut continuer cela jusqu'à
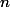
.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 15:06
par pluie2 » 15 Sep 2013, 15:06
Anneauprincipal a écrit:Bonjour,
Pour la première attention au changement d'inégalité quand tu passes à l'inverse.
Si

, alors

, et aussi
^2$)
etc... Il faut continuer cela jusqu'à
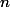
.
vous répondez à la b) ?
car dans la a), on demande de déterminer le plus petit N tel que u_(n+1)/u_n <0.5
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 15:08
par Anneauprincipal » 15 Sep 2013, 15:08
Oui, pour le a) on a

, et pas l'inverse.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 15:10
par pluie2 » 15 Sep 2013, 15:10
a) donc j'en déduis que N est strictement spérieur à -1 ?
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 15:14
par Anneauprincipal » 15 Sep 2013, 15:14
?!!!!!!!!!!!!!!!
N est un entier, pour qu'il soit strictement supérieur à 2x-1, que peut on prendre ?
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 15:17
par pluie2 » 15 Sep 2013, 15:17
oui mais c'est n ici qui est strictement supérieur à 2x-1 et non N
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 15:19
par Anneauprincipal » 15 Sep 2013, 15:19
n est une inconnue dans ton inégalité mais N est le plus petit n entier qui vérifie l'inégalité.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 15:21
par pluie2 » 15 Sep 2013, 15:21
d'accord donc on peut prendre N=2 car si x=1, alors 2-1=1
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 15:22
par Anneauprincipal » 15 Sep 2013, 15:22
Il faut donner une formule pour N en fonction de x. Est ce que partie entière te dit quelque chose ?
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 15:24
par pluie2 » 15 Sep 2013, 15:24
oui la partie entière je connais mais comment la relier à cet exercice ?
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 15:27
par Anneauprincipal » 15 Sep 2013, 15:27
2x-1 est un réel, il suffit de prendre l'entier immédiatement strictement plus grand, donc (la partie entière de 2x-1) +1.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 15:28
par pluie2 » 15 Sep 2013, 15:28
d'accord donc en fait N=[2x-1]+1 ?
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 15:31
par Anneauprincipal » 15 Sep 2013, 15:31
Oui, en prenant la notation de ton cours pour partie entière (il y a bcp de notations différentes)
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 15:34
par pluie2 » 15 Sep 2013, 15:34
oui normalement ce sont des crochets mais sans ceux du haut...
b) donc comme je sais que N=[2x-1]+1 et que n;)[2x-1]+1, je dois montrer que 0
ça me semble assez difficile
d'où dois je commencer
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 16:04
par Anneauprincipal » 15 Sep 2013, 16:04
Tu n'as pas besoin de savoir ce que vaut N. Relis mon premier post, il t'indique l'idée.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 16:13
par pluie2 » 15 Sep 2013, 16:13
vous avez parlez de la partie entière pour N mais ici pour écrire l'inégalité je ne peux pas l'utiliser ? désolé je ne comprends pas
-
Anneauprincipal
- Membre Relatif
- Messages: 147
- Enregistré le: 10 Jan 2009, 13:36
-
 par Anneauprincipal » 15 Sep 2013, 16:20
par Anneauprincipal » 15 Sep 2013, 16:20
Je parlais de la première question pour l'inégalité.
Pour le b), on se fiche de ce que vaut N, il faut remarquer que :
Si

, alors avec


, et aussi
^2$)
etc... Il faut continuer cela jusqu'à
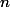
.
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 16:25
par pluie2 » 15 Sep 2013, 16:25
Anneauprincipal a écrit:Je parlais de la première question pour l'inégalité.
Pour le b), on se fiche de ce que vaut N, il faut remarquer que :
Si

, alors avec


, et aussi
^2$)
etc... Il faut continuer cela jusqu'à
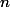
.
d'accord je vais essayer de rédiger et si j'ai un problème je vous le dis
-
pluie2
- Membre Rationnel
- Messages: 521
- Enregistré le: 08 Sep 2013, 13:20
-
 par pluie2 » 15 Sep 2013, 16:31
par pluie2 » 15 Sep 2013, 16:31
je ne comprends pas votre dernière ligne, pourquoi écrivez vous u_(N+2) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
