Signe et variation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 08 Sep 2013, 15:13
par Danbo » 08 Sep 2013, 15:13
Bonjour! :we:
Je dois étudier les signes de la fonction f '(x) et dresser son tableau de variation, mais je ne sais pas comment faire, dois-je utilisé delta?
f(x)= x^3-3x+2
f '(x)= 3x-3

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Sep 2013, 15:20
par Ericovitchi » 08 Sep 2013, 15:20
non delta ça n'est que pour les fonctions du second degré.
ici il te suffit de dériver f(x) (qui vaut f'(x)=3x²-3 et pas ce que tu as écris) et d'étudier son signe.
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 08 Sep 2013, 15:37
par Danbo » 08 Sep 2013, 15:37
merci!
Désolé, j'avais mal recopié --'
Pour trouver son signe il faut regarder si "a" est positif ou négatif? Ici a=3 donc positif.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 08 Sep 2013, 15:52
par Carpate » 08 Sep 2013, 15:52
Danbo a écrit:merci!
Désolé, j'avais mal recopié --'
Pour trouver son signe il faut regarder si "a" est positif ou négatif? Ici a=3 donc positif.
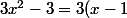(x+1))
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 08 Sep 2013, 16:18
par Danbo » 08 Sep 2013, 16:18
C'est la factorisation de f '(x)
Je comprend pas...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Sep 2013, 16:59
par Ericovitchi » 08 Sep 2013, 16:59
un polynôme du second degré est du signe de a à lextérieur de ses racines et du signe contraire entre. Carpate vient de te montrer que les deux racines étaient -1 et +1 donc tu devrais pouvoir en déduire le signe de cette dérivée.
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 08 Sep 2013, 17:25
par Danbo » 08 Sep 2013, 17:25
Ok, donc:
si x ;) ]-;);-1[ alors f'(x)>0
si x ;) ]-1;+1[ alors f'(x)<0
si x ;) ]1;+;)[ alors f'(x)>0

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Sep 2013, 17:50
par Ericovitchi » 08 Sep 2013, 17:50
oui et donc le tableau de variations s'en déduit.
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 08 Sep 2013, 20:00
par Danbo » 08 Sep 2013, 20:00
ok merci! j'ai réussi a faire mon tableau!
Mais c'est normale que quant je rentre f '(x) dans le mode graph de ma calculatrice, les variation ne sont pas les même?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Sep 2013, 20:37
par Ericovitchi » 08 Sep 2013, 20:37
si tu rentres f'(x) dans le mode graph de ta calculatrice, tu as le graphe de f'(x), pas celui de f(x).
le graphe de f(x) c'est :

et ton tableau de variations :

-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 09 Sep 2013, 07:11
par Danbo » 09 Sep 2013, 07:11
Oui j'ai ça!
Mais la question de mon exercice était de faire le tableau de signe et de variation de la fonction f '(x) et pas celui de f(x) :/

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 09 Sep 2013, 09:27
par Ericovitchi » 09 Sep 2013, 09:27
Et bien tu as l'expression de f'(x), qu'est-ce qui te gêne pour étudier ses variations et le signe ? (le signe tu l'as dans mon tableau d'ailleurs). c'est une simple parabole.
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 09 Sep 2013, 17:39
par Danbo » 09 Sep 2013, 17:39
bah les variations de ton tableau ressemble pas a aux variation d'une parabole :/
Ou alors j'ai mal compris la question ><

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 09 Sep 2013, 22:51
par Ericovitchi » 09 Sep 2013, 22:51
c'est le signe de la dérivée qu'il y a dans le tableau, pas les variations.
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 10 Sep 2013, 17:32
par Danbo » 10 Sep 2013, 17:32
Bah les flèches sont sensé représenté les variations. :o

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 10 Sep 2013, 17:53
par Ericovitchi » 10 Sep 2013, 17:53
oui, les variations de f(x) pas celle de f'(x)
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 12 Sep 2013, 10:31
par Danbo » 12 Sep 2013, 10:31
Donc le tableau de variation de f'(x) serait:
-oo ===> -3 ===> +oo

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 12 Sep 2013, 13:12
par Ericovitchi » 12 Sep 2013, 13:12
non pas du tout.
f'(x)=3x²-3 une parabole tournée vers le haut
-
Danbo
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Sep 2013, 17:16
-
 par Danbo » 12 Sep 2013, 16:13
par Danbo » 12 Sep 2013, 16:13
Je comprend pas sur ma calculatrice en mode graphe la parabole descend jusqu'en -3 puis elle remonte. :/

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 12 Sep 2013, 17:00
par Ericovitchi » 12 Sep 2013, 17:00
oui et bien donc elle est décroissante puis croissante.
c'est peut-être ce que tu as voulu marquer, remarque, c'est le -oo qui m'a gêné, c'est +oo
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités


