Tableau de signe puis valeurs tableau de variation

[benjidu79]

Bonjour,

J'ai une fonction

J'ai calculé sa dérivée

J'ai trouvé les valeurs interdites : 1 et 3
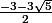
Puis les racines : et

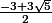
Je factorise le tout et j'ai dressé le tableau de signe.
Puis j'ai dressé le tableau de variation.

Mais le problème, c'est que j'arrive pas à trouver les valeurs à mettre dans ce tableau
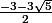
( surtout pour et )
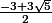
Je connais la méthode ( remplacer la valeur dans l'expression de la fonction) mais je n'arrive pas à l'appliquer.

Pouvez-vous m'aider ?

Merci d'avance

[oscar]

D' abord simpliier f'(x)= -2 (x² +3x-9)/ (x² -4x+3)²
Racines de f' = -1/2(1+v5) et x" = -1/2( 1+v5)
f(x) = ( 2x+3)/ ( x² -4x+3)
Le calculs de f(x) n' est vraiment pas insurmontable
A la rigueur on peut calculer des valeurs approchées

[Sa Majesté]

Tu peux aussi utiliser une petite astuce
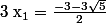
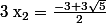
Tu sais que et sont solutions de -x²-3x+9=0 donc pour ces 2 valeurs tu as x²=-3x+9

Quand tu remplaces ça fait
ce qui simplifie un peu

[benjidu79]

Ce que je n'arrive pas à faire c'est de trouver f(-3-3V5/2) et f(-3+3V5/2)
Je n'arrive pas à développer, simplifier puis réduire ...