Algèbre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Mai 2013, 21:29
par barbu23 » 27 Mai 2013, 21:29
Bonsoir à tous,
On pose :

Y'a-t-il une méthode simple qui permet de résoudre le système suivant dans
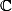
en fonction de

, fixés par avance ?
Voiçi le système dont il est question :

Les inconnues sont

,

et

.
Merci d'avance pour votre aide. :happy3:
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 27 Mai 2013, 21:33
par jlb » 27 Mai 2013, 21:33
bonsoir, à vrai dire je n'ai jamais manié d' exposants complexes mais si c'est licite en multipliant les trois équations tu trouves les valeurs possibles de x et je pense que y et z tombent à la suite [ 1+j+j²=0!!!]
-
quartzmagique
- Membre Relatif
- Messages: 129
- Enregistré le: 18 Mai 2013, 23:35
-
 par quartzmagique » 27 Mai 2013, 22:05
par quartzmagique » 27 Mai 2013, 22:05
bonjour cela se ramène à calculer avec des logarithmes de nombres complexes
pour a non nul alors tu peut poser z=a/(xy)
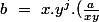^{j^2})
bref cela reviens donc à resoudre un systeme comme ça(les inconnues x et y)
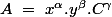
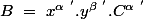
-
quartzmagique
- Membre Relatif
- Messages: 129
- Enregistré le: 18 Mai 2013, 23:35
-
 par quartzmagique » 27 Mai 2013, 22:05
par quartzmagique » 27 Mai 2013, 22:05
bon c'est long mais déjà est-ce que tu voit?
-
quartzmagique
- Membre Relatif
- Messages: 129
- Enregistré le: 18 Mai 2013, 23:35
-
 par quartzmagique » 27 Mai 2013, 22:07
par quartzmagique » 27 Mai 2013, 22:07
j'ai enlevé les barres ça prête à consusion j'ai mis des primes
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Mai 2013, 22:22
par barbu23 » 27 Mai 2013, 22:22
Je ne suis pas très convaincu sur votre argumentation, car d'abord, la question qu'il faut se poser : c'est quoi

? Est ce que ça a un sens ? d'habitude, ça doit être le prolongement analytique de la fonction "réelle"

, non ?
-
quartzmagique
- Membre Relatif
- Messages: 129
- Enregistré le: 18 Mai 2013, 23:35
-
 par quartzmagique » 27 Mai 2013, 22:27
par quartzmagique » 27 Mai 2013, 22:27
barbu23 a écrit:Je ne suis pas très convaincu sur votre argumentation, car d'abord, la question qu'il faut se poser : c'est quoi

? Est ce que ça a un sens ? d'habitude, ça doit être le prolongement analytique de la fonction "réelle"

, non ?
Salut
tu travaille dans Complexe
je comprend pas qu'on te donne ça à faire si tu n'a pas vu
A^B et puis log[A] (B) logarithme de base B en base A avec A et B dans Complexes
peut être que l'exo se simplifie je l'ai pas fait jusqu'au bout mais sinon tu est bien obligé de manipuler ça
x y et z possederaient une infinité de solutions (on est plus dans R)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Mai 2013, 22:31
par barbu23 » 27 Mai 2013, 22:31
quartzmagique a écrit:Salut
tu travaille dans Complexe
je comprend pas qu'on te donne ça à faire si tu n'a pas vu
A^B et puis log[A] (B) logarithme de base B en base A avec A et B dans Complexes
peut être que l'exo se simplifie je l'ai pas fait jusqu'au bout mais sinon tu est bien obligé de manipuler ça
x y et z possederaient une infinité de solutions (on est plus dans R)
Oui, je travaille dans
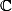
, et

est une fonction "multiforme", c'est pourquoi, je pense que, c'est inutile de dire que
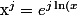} $)
.
-
quartzmagique
- Membre Relatif
- Messages: 129
- Enregistré le: 18 Mai 2013, 23:35
-
 par quartzmagique » 27 Mai 2013, 22:41
par quartzmagique » 27 Mai 2013, 22:41
Salut
mais inutile ?
moi je resoud ça comme ça (bon ton exemple j 'ai pas vu je suis pas allé jusque là dans la resolution ) mais à un moment donné je tomberai sur un truc du genre
si c'est inutile je suppose que tu a une autre methode pour le resoudre alors...
mais tu demande de l'aide je te donne la mienne
là je vais écouter de la zic mais bon je part pas vraiment non plus
je serai curieux de voir comment tu ferai en tout cas si tu a besoin je veux bien le faire un peu
bon jusqu'au bout c'est interdit dans la charte mais au moins un peu
sinon remarque j'ai pas fait l'exo alors si des fois y a des trucs qui se simplifient alors c'est chouette
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Mai 2013, 23:22
par barbu23 » 27 Mai 2013, 23:22
quartzmagique a écrit:Salut
mais inutile ?
moi je resoud ça comme ça (bon ton exemple j 'ai pas vu je suis pas allé jusque là dans la resolution ) mais à un moment donné je tomberai sur un truc du genre
si c'est inutile je suppose que tu a une autre methode pour le resoudre alors...
mais tu demande de l'aide je te donne la mienne
là je vais écouter de la zic mais bon je part pas vraiment non plus
je serai curieux de voir comment tu ferai en tout cas si tu a besoin je veux bien le faire un peu
bon jusqu'au bout c'est interdit dans la charte mais au moins un peu
sinon remarque j'ai pas fait l'exo alors si des fois y a des trucs qui se simplifient alors c'est chouette
J'ai entamé une autre discussion ici, il y'a quelques heures :
http://www.les-mathematiques.net/phorum/read.php?3,843488Tu peux y jeter un oeil si tu veux. :happy3:
-
quartzmagique
- Membre Relatif
- Messages: 129
- Enregistré le: 18 Mai 2013, 23:35
-
 par quartzmagique » 27 Mai 2013, 23:31
par quartzmagique » 27 Mai 2013, 23:31
ah elle est bonne !!!
je suis ban
c'est moi sphinx là bas
merci des fois j'y vais mais je peut pas poster pour aider
bon faut dire que je parlai trop zic aussi entre autre ... :ptdr:
mais bn j'aidai quand même
bon sinon promis je vous saoulerai pas ici
je ferai plus
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 28 Mai 2013, 08:08
par jlb » 28 Mai 2013, 08:08
salut Barbu23 as-tu lu mon post? j'ai l'impression que mon idée fonctionne, qu'en penses-tu ?
(rappel: tu multiplies les 3 équations cela donne x comme racine cubique et après y et z "tombent facilement )

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 28 Mai 2013, 09:04
par chan79 » 28 Mai 2013, 09:04
jlb a écrit:bonsoir, à vrai dire je n'ai jamais manié d' exposants complexes mais si c'est licite en multipliant les trois équations tu trouves les valeurs possibles de x et je pense que y et z tombent à la suite [ 1+j+j²=0!!!]
en multipliant les trois équations, on a donc la condition nécessaire:

et de même

et

Par exemple, si a=-1+i, b=-i et c=1
cela fait trois solutions qui se déduisent les unes des autres par rotation (multiplication par j)
(x1,y2,z1)
(x2,y3,z2)
(x3,y1,z3)

Uploaded with
ImageShack.us
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
? Est ce que ça a un sens ? d'habitude, ça doit être le prolongement analytique de la fonction "réelle"
, non ?
