Exo nombre complexe niveau 5
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 02:34
par sousou33 » 29 Déc 2012, 02:34
bjr
Quelle est la somme des diviseurs propres de 2^n (2^{n+1}-1)
je pensait a 2^n mais ca ne marche pas
merci de votre aide
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 09:38
par Kikoo <3 Bieber » 29 Déc 2012, 09:38
Salut,
On va supposer que 2^{n+1} - 1 est premier, sans quoi l'exo serait un peu bizarre.
Quels sont les diviseurs de 2^n ? Quels sont les diviseurs de 2^{n+1} - 1 ?
Peux-tu en déduire l'ensemble des diviseurs de 2^n(2^{n+1} - 1) ?
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 12:55
par sousou33 » 29 Déc 2012, 12:55
Les diviseurs de 2^n sont :
2^0 , 2^1 , 2^2 , ... 2^n
Les diviseurs de 2^{n+1} - 1 sont :
1 , 3 , 7 , ...
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 13:00
par sousou33 » 29 Déc 2012, 13:00
et oui 2^{n+1} - 1 est premier j'ai oubier de le préciser
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 13:10
par Kikoo <3 Bieber » 29 Déc 2012, 13:10
sousou33 a écrit:Les diviseurs de 2^n sont :
2^0 , 2^1 , 2^2 , ... 2^n
Les diviseurs de 2^{n+1} - 1 sont :
1 , 3 , 7 , ...
Non, si 2^{n+1} - 1 est premier, on ne peut pas trouver d'autres diviseurs que lui-même et 1 !
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 13:14
par sousou33 » 29 Déc 2012, 13:14
Donc cela signifie que les diviseur de 2^n (2^{n+1}-1) sont
1 , 2 , 2^2 , ... 2^n , 2^{n+1}-1 ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 13:16
par Kikoo <3 Bieber » 29 Déc 2012, 13:16
Non.
D'abord, il faut considérer les diviseurs de 2^n, puis les diviseurs de 2^{n+1}-1 puis du produit de ces deux nombres !
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 13:21
par sousou33 » 29 Déc 2012, 13:21
Les diviseurs de 2^n sont :
2^0 , 2^1 , 2^2 , ... 2^n
Les diviseurs de 2^{n+1} - 1 sont :
(2^{n+1} - 1) , 2(2^{n+1} - 1) , 2^2(2^{n+1} - 1) , ... , 2^n(2^{n+1} - 1) ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 13:23
par Kikoo <3 Bieber » 29 Déc 2012, 13:23
sousou33 a écrit:Les diviseurs de 2^{n+1} - 1 sont :
(2^{n+1} - 1) , 2(2^{n+1} - 1) , 2^2(2^{n+1} - 1) , ... , 2^n(2^{n+1} - 1) ?
Je le répète, 2^{n+1} - 1 est premier. Cela signifie qu'il n'a pas d'autre diviseurs que lui-même et 1 !

Donc ?
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 13:28
par sousou33 » 29 Déc 2012, 13:28
ah oui il est divisible par 1 et 2^{n+1} - 1
les diviseur de 2^n (2^{n+1}-1) sont
2^0 , 2^1 , 2^2 , ... 2^n , 2^{n+1} - 1 , 2(2^{n+1} - 1) , 2^2(2^{n+1} - 1) , ... , 2^n(2^{n+1} - 1)
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 13:33
par Kikoo <3 Bieber » 29 Déc 2012, 13:33
sousou33 a écrit:ah oui il est divisible par 1 et 2^{n+1} - 1
les diviseur de 2^n (2^{n+1}-1) sont
2^0 , 2^1 , 2^2 , ... 2^n , 2^{n+1} - 1 , 2(2^{n+1} - 1) , 2^2(2^{n+1} - 1) , ... , 2^n(2^{n+1} - 1)
Voilà

Je pense bien que le compte est bon.
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 13:35
par sousou33 » 29 Déc 2012, 13:35
Merci beaucoup
Et comment prouver que 2^n *(2^{n+1}-1) est parfait sachant 2^{n+1} - 1 est premier ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 13:36
par Kikoo <3 Bieber » 29 Déc 2012, 13:36
Euh ben tu calcules la somme de ses diviseurs.
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 13:41
par sousou33 » 29 Déc 2012, 13:41
donc je fait 2^0+2^1+2^2+...+(2^{n+1} - 1)+ 2(2^{n+1} - 1) + 2^2(2^{n+1} - 1) + ... + 2^n(2^{n+1} - 1)
C'est impossible a calculer ca ^^'
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 15:01
par Kikoo <3 Bieber » 29 Déc 2012, 15:01
Désolé je me suis trompé !
En fait, les diviseurs de
) autres que lui-même
autres que lui-même sont :
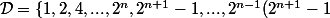\})
Du coup, on a
+\sum_{k=0}^{n}2^k=\(2^{n+1}-1\)\(\frac{2^n-1}{2-1}\)+...)
Je te laisse mener le calcul, tu dois tomber sur
)
, c'est-à-dire l'entier de départ !
PS : il n'est pas sur les complexes cet exo, c'est de l'arithmétique !
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 15:19
par sousou33 » 29 Déc 2012, 15:19
Je n'arrive pas a retomber sur le resultat qu'on doit obtenir
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Déc 2012, 15:30
par Kikoo <3 Bieber » 29 Déc 2012, 15:30
Ah bon ? Et pourtant il ne reste presque plus rien...
Que vaut la somme géométrique

?
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 18:34
par sousou33 » 29 Déc 2012, 18:34
beh ca vaut 1
-
sousou33
- Membre Naturel
- Messages: 14
- Enregistré le: 14 Avr 2012, 09:48
-
 par sousou33 » 29 Déc 2012, 18:40
par sousou33 » 29 Déc 2012, 18:40
nan ce n'est pas ca ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
