Exo sur la méthode de Cardan nombre complexe

[jeanfifirai]

Bonsoir, j'ai de grosses difficultés à résoudre un exercice, déjà parce que j'ai du mal à débuté mais surtout on vient de commencer les nombres complexes depuis 2 semaines.
On considère dans cet exercice l'équation suivante : x³ -15x -4 = 0

I) a) On suppose : u+v=x
3uv=15

Je dois montrer que avec ce couple on a u³v³ = 125. C'est bête j'ai l'impression que c'est tout simple mais je ne vois pas comment aboutir à ce résultat...


b) Je dois montrer que l'équation s'écrit u³ + v³ = 4

Voilà si je pouvais avoir un peu d'aide pour débuter cet exo merci !

[mathelot]

Bonsoir, j'ai de grosses difficultés à résoudre un exercice, déjà parce que j'ai du mal à débuté mais surtout on vient de commencer les nombres complexes depuis 2 semaines.
On considère dans cet exercice l'équation suivante : x³ -15x -4 = 0

I) a) On suppose : u+v=x
3uv=15

Je dois montrer que avec ce couple on a u³v³ = 125. C'est bête j'ai l'impression que c'est tout simple mais je ne vois pas comment aboutir à ce résultat...


b) Je dois montrer que l'équation s'écrit u³ + v³ = 4

Voilà si je pouvais avoir un peu d'aide pour débuter cet exo merci !

cette équation est célèbre !! Elle a été présentée par l'héritier de J.Cardan (Tartaglia ?)
pour présenter les nombres imaginaires...



développe et écris

puis associe 3uv(u+v) et -15(u+v)

ca va ddonner une condition suffisante (pas forcément nécessaire)

sur et pour que la somme totale soit nulle.

après tu écris l'équation du second degré vérifiée par les cubes.

[mathelot]

Bonsoir, j'ai de grosses difficultés à résoudre un exercice, déjà parce que j'ai du mal à débuté mais surtout on vient de commencer les nombres complexes depuis 2 semaines.
On considère dans cet exercice l'équation suivante : x³ -15x -4 = 0

on pose x=u+v






On pose



Il s'agit d'écrire une équation du second degré vérifiée par et

[jeanfifirai]

cette équation est célèbre !! Elle a été présentée par l'héritier de J.Cardan
pour présenter les nombres imaginaires...



développe et écris

puis associe 3uv(u+v) et -15(u+v)

ca va ddonner une condition suffisante (pas forcément nécessaire)

sur et pour que la ssomme totale soit nulle.

après tu écris l'équation du second degré vérifiée par les cubes.

Je ne comprend pas comment tu as trouvé (u+v)³ -15(u+v)-4=0
En développant (u+v)³ j'obtiens u³+3uv+v³

Et qu'entends tu par "associer" ?

[mathelot]

[jeanfifirai]

D'accord, donc maintenant pour prouver que u³v³=125 je sais que :

(u+v)³-15(u+v)-4=0

Je sais aussi que (u+v)³= u³+3u²v+3uv²+v³

Et donc u³+3u²v+3uv²+v³ - 15(u+v)-4=0

[fatal_error]

salut,

pour montrer que
u^3v^3=125

tu peux juste partir de
3uv=15
<=>uv=5
=>(uv)^3=5^3

[mathelot]

est ce que tu t'en sors ?





reste plus qu'à résoudre

heureusement, c'est là où l'équation est un cas d'école,

le est un carré parfait:

[paquito]

Ce qui me surprend, c'est que l'équation admet 3 racines réelles et que dans ce cas la méthode de Cardan conduit à des calculs infects alors qu'au niveau lycée la méthode trigonométrique offre un exemple surprenant, mais efficace.
Que va faire jeanfifirai avecet alors qu'il viens de commencer les complexes?
A moins que l'énoncé s'arrête à montrer que ???

Je me sens obliger de donner une solution: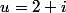 et d'où 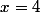, puis de lui faire vérifier que vérifie 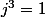ainsi que et que donc si l'on prend les deux solutions donnéeset , et vont en donner une seconde et et la troisième.

[mathelot]

@paquito:

tu fais un anachronisme

Cette équation a été présentée avant l'invention des nombres complexes.

A un moment des mathématiques où ils avaient le signe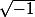 mais pas l'imaginaire

Ils n'avait pas la représentation des complexes avec les points le plan (qui date d'Argand) ni la notation qui vient d'Euler.

Tout ce quils savaient c'est qu'en posant
, ils trouvaient 4 comme vraie solution.

[paquito]

Le rapport avec l'exercice posé? On connait maintenant les nombres complexes et écrire a été une étape; historiquement les nombres complexes ont été admis lorsqu'ils ont eu une interprétation géométrique; cela n'a rien à voir avec notre problème qui conduit à rechercher des racines cubiques alors que la recherche des racines carrées est déjà hors programme! Et c'est parce que j'ai constaté que 4 était racine que j'ai trouvé une solution très simple; remplace 15 par 16 et tu vas comprendre le problème; de toute façon; pourquoi ne pas traiter d'abord le cas d'une seule solution réelle, puis voir avec la méthode trigonométrique qui est très intéressante le cas de 3 solutions réelles; la méthode de cardan permet aussi de trouver les solutions non-réelles, mais c'est tellement "complexe" que ce n'est même pas enseigné dans le supérieur; donc cet exercice, même si on sait le résoudre est pédagogiquement à côté de la plaque!

[mathelot]

Le rapport avec l'exercice posé?

l'équation du second degré donne

et

on vérifie que


et


on trouve la solution réelle

Cette équation a une histoire,

elle a été présentée par Tartaglia ou Cardano à un moment où ils ne connaissaient

ni les nombres complexes, ni les affixes, ni la notation

mais seulement . Ils souhaitaient des carrés négatifs pour résoudre

les équations mais sans savoir où ça allait conduire,ie, à toute l'analyse complexe

que l'on connait actuellement.

[mathelot]

Le rapport avec l'exercice posé? On connait maintenant les nombres complexes et écrire a été une étape; historiquement les nombres complexes ont été admis lorsqu'ils ont eu une interprétation géométrique; cela n'a rien à voir avec notre problème qui conduit à rechercher des racines cubiques alors que la recherche des racines carrées est déjà hors programme! Et c'est parce que j'ai constaté que 4 était racine que j'ai trouvé une solution très simple; remplace 15 par 16 et tu vas comprendre le problème; de toute façon; pourquoi ne pas traiter d'abord le cas d'une seule solution réelle, puis voir avec la méthode trigonométrique qui est très intéressante le cas de 3 solutions réelles; la méthode de cardan permet aussi de trouver les solutions non-réelles, mais c'est tellement "complexe" que ce n'est même pas enseigné dans le supérieur; donc cet exercice, même si on sait le résoudre est pédagogiquement à côté de la plaque!

Quand je t'ai répondu, je n'avais pas lu ton texte. Ce que tu ne vois pas , ou que tu négliges,

c'est une équation particulière, qui a une histoire.

Si tu apprends à faire du vélo sur un Grand Bi (les vélos avec la roue avant immense)

c'est pas pareil que d'apprendre à faire du vélo avec un bike. Tu te resitues

dans un contexte historique. Cette équation est un monument historique.

Ceci écrit, la méthode de Cardan , quand tu es confronté dans certains cas

à des arctangentes, je suis d'accord avec toi que ce n'est pas une bonne méthode de

résolution . Je suis aussi d'accord avec toi que les racines cubiques, ce n'est pas top.

[paquito]

l'équation du second degré donne

et

on vérifie que


et


on trouve la solution réelle

Cette équation a une histoire,

elle a été présentée par Tartaglia ou Cardano à un moment où ils ne connaissaient

ni les nombres complexes, ni les affixes, ni la notation

mais seulement . Ils souhaitaient des carrés négatifs pour résoudre

les équations mais sans savoir où ça allait conduire,ie, à toute l'analyse complexe

que l'on connait actuellement.

j'aime beaucoup le "on vérifie que...." l'équation a une racine connue! Je donne à mes élèves, en leur parlant des duels où s"affrontaient les grands mathématiciens de la renaissance un exemple pas trop
compliqué: comment factoriser
1°duelliste: , le public reste sur sa faim...

2°duelliste:je vais utiliser un nombre qui n'existe pas! je le note et il vérifie donc , on calcule normalement, par exemple ; donc je peux écrire:
, après avoir regroupé les termes comme il fallait.

Le public est ému; il sent bien qu'il a assisté à quelque chose d'important....

Tout ça, c'est du cinéma et ne correspond pas à la vérité historique, mais je me vois mal présenter les nombres complexes à partir d'une équation de degré 3; il faut quand même rester raisonnable!

[jeanfifirai]

Bonsoir, j'ai eu des problèmes de connexion internet aujourd'hui !
Je n'ai pas tout suivi dans votre débat mais sachez que j'ai finalement réussi à trouver les réponses à ma question ! Donc merci

J'ai encore une question à vous poser plus loin dans l'exo : je dois développer (2-sqrt(-1))³ et (2+sqrt(-1))³

Problème je ne sais pas développer avec des cubes... j'ai essayé de trouver avec la calculatrice mais évidemment je suis tombé sur un os même si je m'en doutais (la racine de -1 ne se calcule pas)

[mathelot]

par double distributivité





les régles de calcul pour sont de remplacer dès que possible

par

[paquito]

tu dis trouver et donc

et sont un couple solution , mais u^3=2+11i admet 3 solutions:

si l'on pose,



donc . donc, s'il y a 3 solutions pour u et 3 pour v, comment trouver les solutions ?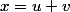

En fait on sais que x est réel et il n y a alors que 3 possibilités pour associer u et v; ils doivent être conjugués et donc est bien une solution.

Tout ça me semble un peu trop compliqué quand même!!