Hello tout le monde,
j'aurai besoin d'un petit coup de main pour cet exercice:
Soit une fonction à deux variable
f(x,y)= exp(xy)*(x+xy-1)
1. Quel est le domaine de cette fonction ?
2. Calculer le gradient de f en tout point (x,y)
3. Déterminer l'ensemble des points stationnaires
4. Calculer la matrice hessienne en tout point (x,y)
5. On considère en particulier le cas oÙ Y = -1 on note
g(x) = f(x,-1)
a) tracer le graphe de cette fonction. Cette fonction est-elle bijective, et si oui sur quels ensemble ?
b) Quelle est sa fonction réciproque ? Tracer son graphe.
Voila ce que j'ai réussi à répondre:
1) R^2
2) df/dx = exp(xy)*(xy+xy^2+1) et df /dy = exp(xy)*(x^2+x^2y)) le gradient correspond au 2 valeurs trouvées
3) ??? je sais juste qu'il faut poser le gradient = (0,0) mais je ne vois vraiment pas comment résoudre le système
4) H= exp(xy) *( xy^2+ xy^3 +2y +y^2 ??? ( je n'arrive pas à trouver la dérivée mixte)
??? idem x^3 + x^3y+x^2 )
5 a) je suis bloquée
5 b) idem vu que la question 5.b est un corollaire.
Merci d'avance pour votre aide
Dérivée partielle
7 messages
- Page 1 sur 1
Salut !
Déjà, donc, résous le système :
donc, résous le système :
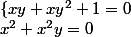 .
.
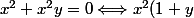=0 \Longleftrightarrow x=0\ {\rm ou}\ y= -1)
Doubi a écrit:(...)
f(x,y)= exp(xy)*(x+xy-1)
(...)
3. Déterminer l'ensemble des points stationnaires
(...)
??? je sais juste qu'il faut poser le gradient = (0,0) mais je ne vois vraiment pas comment résoudre le système
(...)
Déjà,
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Déjà,donc, résous le système :
.
Hey !
merci pour ton aide j'ai refais le calcul et tout est en ordre ! ( en fait je m'étais trop compliqué la vie dans le système que j'avais posé...)
J'ai réussi la question 5 a et b il me manque plus qu'à trouver la dérivée mixte et j'aurai enfin mon exercice complet si qqn pourrait m'éclairer ça serait génial !
Cordialement
Doubi a écrit:Hey !
merci pour ton aide j'ai refais le calcul et tout est en ordre ! ( en fait je m'étais trop compliqué la vie dans le système que j'avais posé...)
J'ai réussi la question 5 a et b il me manque plus qu'à trouver la dérivée mixte et j'aurai enfin mon exercice complet si qqn pourrait m'éclairer ça serait génial !
Cordialement
Quand tu dis dérivée mixte, tu veux parler de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Doubi a écrit:Exactement !
Or tu as déjà calculer
Donc en dérivant par rapport à
:++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
