Df=R
tql f(x)=1 si x dans Q et f(x)=0 si x dans R-Q
démontrez que f n'est continue en aucun point de R :hein:
Continuité terminal s
10 messages
- Page 1 sur 1
@yahumi
Pistes de travail :
Utilise le Théorème :
si une fonction f est continue sur IR et si une suite) de IR converge vers un nombre L alors la suite
de IR converge vers un nombre L alors la suite ) définie par
définie par 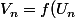) converge vers le nombre f(L)
converge vers le nombre f(L)
Et utilise le fait que Q est dense dans IR
Question
Sais tu ce que veut dire Q est dense dans IR ?
ou
ce qui revient au même mais qui est plus "imagé" :
Sais tu que pour tout réel , il existe 2 suites
, il existe 2 suites ) et
et )
1) qui sont des suites de nombre rationnel donc des suites de nombre appartenant à Q
2) telles que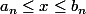 pour tout n
pour tout n
3) ces 2 suites) et
et ) convergent vers le réel
convergent vers le réel 
ps)
La suite) est très connue car c'est le développement décimal du réel
est très connue car c'est le développement décimal du réel 
Pistes de travail :
Utilise le Théorème :
si une fonction f est continue sur IR et si une suite
Et utilise le fait que Q est dense dans IR
Question
Sais tu ce que veut dire Q est dense dans IR ?
ou
ce qui revient au même mais qui est plus "imagé" :
Sais tu que pour tout réel
1) qui sont des suites de nombre rationnel donc des suites de nombre appartenant à Q
2) telles que
3) ces 2 suites
ps)
La suite
ptitnoir a écrit:@yahumi
Essaie d'être un peu plus précis , car j'ai comme un doute car cette démo n'est pas évidente
Peux tu préciser
1) la définition dont tu parles
2) expliquer comment à partir de cette définition tu peux répondre à cet exo ( explique en quelques phrases , sans détailler )
ok, si a dans Q alors il existe un x dans R/Q (f(x)-f(a) )=(a)sup à epsilon qui est égale à (a/2) les ()=valeur absolue .....et de meme pour x dans Q
Bonjouryahumi a écrit:ok, si a dans Q alors il existe un x dans R/Q (f(x)-f(a) )=(a)sup à epsilon qui est égale à (a/2) les ()=valeur absolue .....et de meme pour x dans Q
Je ne comprends pas quelle propriété tu utilises pour écrire que
si
(*) j'ai remplacé dans ton message le |a| par |x-a|
car je pense que tu as du faire une faute de frappe en écrivant ce message
avec la fonction
définie suret telle que
sialors
=1)
sialors
=0)
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
