Niveau Fin terminal / Début L1

[Cryptocatron-11]

Petit exercice niveau fin terminal - début L1.

Combien y'a t'il de nombre compris entre 0 et 1000 qui comporte au moins un 7 ?

[Zweig]

Salut,

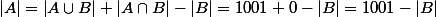
Soit A = {entiers compris entre 0 et 1000 comprenant au moins un chiffre 7} et B = {entiers compris entre 0 et 1000 ne comprenant aucun chiffre 7}. On veut déterminer . On dispose de l'égalité suivante : [CENTER][/CENTER]

Il ne reste plus qu'à faire du dénombrement sur B :lol3:.

[Cryptocatron-11]

C'était la manière la plus simple à faire pour pas s’embêter. Mais j'en voyais une un peu plus prise de tête. Un peu plus du style algo si tu vois laquelle =)

Au final on trouve avec les deux astuces 271 nombres qui comportent au moins un 7

[Zweig]

Les entiers entre 10 et 999 sont de la forme abc. On compte combien y a d'entiers avec un chiffre 7, puis deux chiffres 7 et enfin trois chiffres 7 (en on rajoute + 1 à ce résultat)

[Cryptocatron-11]

On dénombre tous les chiffres qui ont pour centaine 7 . Puis tout ceux qui ont 7 en dizaine en tachant de ne pas tenir compte de ce qui ont pour centaine 7 . Enfin on finit par compter tout ceux qui finissent par 7 en enlevant ceux qui ont déjà un 7 pour centaine et/ou pour dizaine. :lol3:

c'est plus facile à voir sur un arbre .

[Zweig]

C'est ce que je viens de dire, non ?

[Cryptocatron-11]

C'est ce que je viens de dire, non ?

Ah dsl j'avais pas compris :ptdr:

[SaintAmand]

Au final on trouve avec les deux astuces 271 nombres qui comportent au moins un 7

Donc 9^3 nombres sans utiliser le chiffre 7...