Oui, c'est possible et en fait ce que tu demande est plus ou moins équivalent à la recherche d'une partie de R (à savoir
)
) qui soit fermée, d'intérieur vide, mais de mesure non nulle.
L'exemple classique d'une telle partie de R est celui de des
ensembles de Cantor généralisés qui permet aisément de construire une fonction ayant les propriétés demandées :
On fixe un

et part de
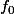
qui est la fonction nulle sur [0,1].
On construit le graphe de

en partant de celui de
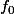
et en remplaçant le segment horizontal de longueur

centré au milieu de [0,1] par les deux autres cotés du triangle équilatéral qui "complètent" le segment en question (j'espère que je suis clair...)
De même, on construit le graphe de

en partant de celui de

et en remplaçant les deux segments horizontaux de longueur

centré au milieu des deux segments horizontaux du graphe de

par les deux autres cotés des triangles équilatéraux qui "complètent" ces segments.
Etc...
Il est clair que la suite
_{n\geq 0})
converge normalement vers une fonction

qui est continue, "sans plateau" (car
)
est fini pour
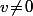
et
)
est d'intérieur vide) mais par contre elle n'est pas "de constance nulle" car
\!=\!1\!-\!s>0)
.
