Borne inf
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
timo9owa
- Membre Naturel
- Messages: 25
- Enregistré le: 22 Sep 2012, 12:48
-
 par timo9owa » 22 Sep 2012, 21:07
par timo9owa » 22 Sep 2012, 21:07
soit Ap={m+n*sqrt2 \ m,n de Z} et Ap+ ={x de Ap \ x>0}
determiner inf(A2+) :hein: :hein: :hein:
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 23 Sep 2012, 07:44
par wserdx » 23 Sep 2012, 07:44
N'y aurait-il pas dans ton exercice une indication du genre : étudier la suite
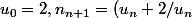/2)

est à valeurs rationnelles on a donc


et

entiers.
Que peux-tu dire alors de

?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 23 Sep 2012, 10:27
par Maxmau » 23 Sep 2012, 10:27
timo9owa a écrit:soit Ap={m+n*sqrt2 \ m,n de Z} et Ap+ ={x de Ap \ x>0}
determiner inf(A2+) :hein: :hein: :hein:
Bj
Examine les puissances de. 2 - rac(2)
-
timo9owa
- Membre Naturel
- Messages: 25
- Enregistré le: 22 Sep 2012, 12:48
-
 par timo9owa » 23 Sep 2012, 11:55
par timo9owa » 23 Sep 2012, 11:55
Maxmau a écrit:Bj
Examine les puissances de. 2 - rac(2)
dans la question precedente on a montré que (sqrt(2)-1)^(n) in A2+ et que m(sqrt(2)-1)^(n) in A2 tel que m in Z :help: :help: :help: :help: :help:
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 23 Sep 2012, 12:29
par wserdx » 23 Sep 2012, 12:29
Bon donc tu as une famille d'éléments qui sont dans l'ensemble dont tu cherches la borne inférieure.
Que devient
^n)
quand

tend vers l'infini?
-
timo9owa
- Membre Naturel
- Messages: 25
- Enregistré le: 22 Sep 2012, 12:48
-
 par timo9owa » 23 Sep 2012, 12:30
par timo9owa » 23 Sep 2012, 12:30
wserdx a écrit:Bon donc tu as une famille d'éléments qui sont dans l'ensemble dont tu cherches la borne inférieure.
Que devient
^n)
quand

tend vers l'infini?
0 a mon avis
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 23 Sep 2012, 12:35
par wserdx » 23 Sep 2012, 12:35
Oui, et ça te donne une piste pour la borne inférieure ?
-
timo9owa
- Membre Naturel
- Messages: 25
- Enregistré le: 22 Sep 2012, 12:48
-
 par timo9owa » 23 Sep 2012, 12:36
par timo9owa » 23 Sep 2012, 12:36
wserdx a écrit:Oui, et ça te donne une piste pour la borne inférieure ?
0????????????????????????????????
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 23 Sep 2012, 12:43
par wserdx » 23 Sep 2012, 12:43
Oui, peux-tu ébaucher un raisonnement pour conclure ou est-ce que tu bloques encore?
-
timo9owa
- Membre Naturel
- Messages: 25
- Enregistré le: 22 Sep 2012, 12:48
-
 par timo9owa » 23 Sep 2012, 12:44
par timo9owa » 23 Sep 2012, 12:44
wserdx a écrit:Oui, peux-tu ébaucher un raisonnement pour conclure ou est-ce que tu bloques encore?
pour le raisonnement non mais pour le resultat je crois que je l'ai trouvé
:hein:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
