Polynômes

par **MoRBT** » 28 Mai 2012, 15:40

Bonjour,

Je n'arrive pas à trouver l'idée pour résoudre la première question de l'exercice suivant:

soit

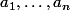
des réels distincts.
1) Calculer

2) On pose

Calculer

Je vous remercie par avance.

par **girdav** » 28 Mai 2012, 16:26

As-tu essayé pour n=2, 3 pour avoir une idée pour le cas général ?

par **MoRBT** » 28 Mai 2012, 18:24

J'ai essayé mais je n'ai pas pu avoir l'idée générale.
est-ce que c'est juste ce que j'ai eu pour n=3

Je vois que dans le cas général ça s'écrit comme ça

où

Pourriez-vous m'aider d'avantage.

par **girdav** » 28 Mai 2012, 19:47

Que vaut-il aux

?

par **MoRBT** » 28 Mai 2012, 20:38

Il vaut 1 aux

Est-ce que c'est ça ce qui est demandé dans l'exo ?? c'est à dire évaluer la formule donnée aux

Pour la question deux j'ai trouvé ça

, est-ce c'est juste ou il faut encore simplifier ?

Merci beaucoup Girdav.

par **girdav** » 28 Mai 2012, 20:57

Et combien sont les a_i par rapport au degré du polynôme ?

par **MoRBT** » 28 Mai 2012, 21:09

girdav a écrit:Et combien sont les a_i par rapport au degré du polynôme ?

il y a

élément

et le degré des polynômes

est

.

Je n'ai pas compris où tu veux arriver avec cette question, je pense qu'il y a une propriété que je ne connais pas.

par **girdav** » 28 Mai 2012, 21:10

Combien de racines a P-1?

par **MoRBT** » 28 Mai 2012, 21:25

Je n'ai pas compris :)

par **alm** » 28 Mai 2012, 21:47

MoRBT a écrit:Je n'ai pas compris

Du courage! il ne te reste rien pour arriver grâce aux indications de girdav ..

un polynôme qui a plus de racines que son degré est forcément nul ... n'est ce pas ?

par **MoRBT** » 28 Mai 2012, 22:05

girdav a écrit:Combien de racines a P-1?

Mais le polynôme

a

racines et il est de degré

.

Je ne comprends pas du quel polynôme parles-tu ?

Merci d'avance Girdav

par **alm** » 28 Mai 2012, 22:15

MoRBT a écrit:Mais le polynôme a racines et il est de degré .

Je ne comprends pas du quel polynôme parles-tu ?

Merci d'avance Girdav

Regarde plutôt du coté du polynôme

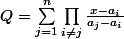
c'est ce polynôme qui verifie

pour tout

donc le polynôme

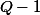
posséde

racines distinctes et son degré est au plus

par **MoRBT** » 28 Mai 2012, 23:57

Je vous remercie,

Et pour la deuxième question ce que c'est varie ce que j'ai fait ?

par **alm** » 29 Mai 2012, 00:23

MoRBT a écrit:Je vous remercie,

Et pour la deuxième question ce que c'est varie ce que j'ai fait ?

Salut MoRBT
je crois que c'est vrai mais tu dois pousser encore ta recherche : il faut trouver

.

Polynômes

Polynômes

Qui est en ligne