Produit scalaire

[Cryptocatron-11]

Bonjour,

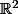
Soit (x,y) les coordonnées d'un vecteur appartenant à dans une base orthonormale

On a grâce à l'opération algébrique "produit scalaire" :

(x,y).(x,y)= xx + yy

Ma question est : cette égalité se démontre t-elle ou alors c'est juste un truc à admettre comme une simple opération ?

[Nightmare]

Hello,

ça dépend de ta définition du produit scalaire. Quelle est-elle?

[Cryptocatron-11]

Pour moi le produit scalaire c'est une opération algébrique entre deux vecteurs et qui donne la somme des produits des coordonnées des 2 vecteurs. Mais ça c'est dans une base orthonormale.

[Nightmare]

N'est-ce pas exactement ce qui est écrit dans ton premier post?

[Cryptocatron-11]

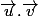
Bah on a u et v deux vecteurs et par définition le produit scalaire de ces deux vecteurs c'est le nombre réél définie par :

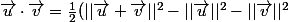[Nightmare]

Admettons, ce peut être une définition. Peux-tu à partir de celle-ci prouver la propriété de ton premier post?

[Blueberry]

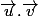
Bah on a u et v deux vecteurs et par définition le produit scalaire de ces deux vecteurs c'est le nombre réél définie par :

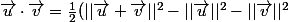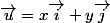
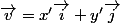
Bah alors tu supposes que et avec et
Et pis tu calcules, bah c'est pas plus compliqué que ça.

[Cryptocatron-11]

Admettons, ce peut être une définition. Peux-tu à partir de celle-ci prouver la propriété de ton premier post?

Oui sans problème, sauf que je serais obligé de poser

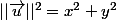
[Nightmare]

Pourquoi le "poser" ?

Quelle est ta définition de la norme d'un vecteur?

[Cryptocatron-11]

OK. Ouais c'est vrai que c'est sa norme ...

Mais pour en revenir à la définition, tu dis "Admettons, ce peut être une définition" , tu en as une autre ?

[vincentroumezy]

Le produit scalaire est une forme bilinéaire symétrique définie positive en est une.

[Nightmare]

Le produit scalaire est une forme bilinéaire définie positive en est une.

Il manque "symétrique" et nous parlons ici du produit scalaire usuel dans R², donc la définition est trop générale.

Cryptocatron-11 > N'as-tu jamais rencontré de définition géométrique du produit scalaire?

[vincentroumezy]

Oups, corrigé.

[Cryptocatron-11]

Cryptocatron-11 > N'as-tu jamais rencontré de définition géométrique du produit scalaire?

Si surement mais du niveau première/term. On en a pas beaucoup reparlé depuis. Là on le réutilise car on bosse sur les ev normés, espace de hilbert ...