1.exprimer (cos ABC) ² + (sin ABC)² en fonction des cotés du triangle
= (AB/BC)² + (AC/BC)²
= ABxAB/BCxBC + ACxAC/BCxBC
= AB² + AC²/ BCpuissance4
est ce juste
2. ecrire l'expression sous la forme d'un seul quotient
j'ai pas compris
Sinus et cosinus
6 messages
- Page 1 sur 1
emredemir a écrit:1.exprimer (cos ABC) ² + (sin ABC)² en fonction des cotés du triangle
= (AB/BC)² + (AC/BC)²
= ABxAB/BCxBC + ACxAC/BCxBC
= AB² + AC²/ BCpuissance4
est ce juste
2. ecrire l'expression sous la forme d'un seul quotient
j'ai pas compris
ATTENTION !!!!! Ta 3ème ligne de calcul est FAUSSE ! Tu additionnes 2 fractions au même dénominateur qui est BC*BC = BC² La somme n'est pas "sur BC puissance4" comme tu l'as écrit !
Mais bien "sur BC puissance2" c'est à dire = (AB² + AC²) / BC².
Or, tu sais que AB² + AC² = ...... Donc (AB² + AC²) / BC² = .
et (cosABC)² + sin(ABC)² = . Nouvelle belle formule de trigonométrie !
A TOI !
jeffb952 a écrit:ATTENTION !!!!! Ta 3ème ligne de calcul est FAUSSE ! Tu additionnes 2 fractions au même dénominateur qui est BC*BC = BC² La somme n'est pas "sur BC puissance4" comme tu l'as écrit !
Mais bien "sur BC puissance2" c'est à dire = (AB² + AC²) / BC².
Or, tu sais que AB² + AC² = ...... Donc (AB² + AC²) / BC² = .
et (cosABC)² + sin(ABC)² = . Nouvelle belle formule de trigonométrie !
A TOI !
= (AB/BC)² + (AC/BC)²
= ABxAB/BCxBC + ACxAC/BCxBC
= (AB² + AC²) / BC ²
= j'ai pas trouvé
je ne comprend pas
emredemir a écrit:= (AB/BC)² + (AC/BC)²
= ABxAB/BCxBC + ACxAC/BCxBC
= (AB² + AC²) / BC ²
= j'ai pas trouvé
je ne comprend pas
Ta dernière formule , qui est exacte : = (AB² + AC²) / BC²
Mais tu sais que AB² + AC² = BC² d'après le théorème de Pythagore dans ton triangle ABC rectangle en A !
Donc ton quotient (AB² + AC²) / BC² devient BC² / BC² et le résultat est égal à .....
1 bien sûr !
D'où la formule de trigo que tu as démontrée : (cosABC)² + (sinABC)² = 1.
Compris ? A TOI !
jeffb952 a écrit:Ta dernière formule , qui est exacte : = (AB² + AC²) / BC²
Mais tu sais que AB² + AC² = BC² d'après le théorème de Pythagore dans ton triangle ABC rectangle en A !
Donc ton quotient (AB² + AC²) / BC² devient BC² / BC² et le résultat est égal à .....
1 bien sûr !
D'où la formule de trigo que tu as démontrée : (cosABC)² + (sinABC)² = 1.
Compris ? A TOI !
= (AB/BC)² + (AC/BC)²
= ABxAB/BCxBC + ACxAC/BCxBC
= (AB² + AC²) / BC²
= BC² / BC²
= 1
la réponse est 1
est ce juste
2. écrire sous la forme d'un seul quotient
tan/tan = 1
est ce juste
3. En utilisant le théoreme de pyhagore , simplifier le quotient
j'ai pas compris
4.Que peut on dire de (cos ABC)² + (sin ABC) ²
pas trop compris
autre méthode
écris Pythagore

on divise les deux membres de l'égalité par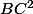

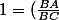^2 +(\frac{AC}{BC})^2)
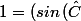)^2 +(cos \, (\hat{C}))^2=(cos \, (\hat{B}))^2 +(sin \, (\hat{B}))^2)
en écrivant les formules sans dessin, on se rend compte que l'on n'a pas besoin de "voir" pour écrire
des maths
autre chose
trace un triangle rectangle pythagoricien de côtés (3,4,5)
l'hypoténuse vaut 5.
calcule les sinus et cosinus des angles qui valent 0,6 et 0,8.
écris Pythagore
on divise les deux membres de l'égalité par
en écrivant les formules sans dessin, on se rend compte que l'on n'a pas besoin de "voir" pour écrire
des maths
autre chose
trace un triangle rectangle pythagoricien de côtés (3,4,5)
l'hypoténuse vaut 5.
calcule les sinus et cosinus des angles qui valent 0,6 et 0,8.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
