Changement de base 3D -> 2D

[timoch]

Bonjour,

J'ai un ensemble de points dont les coordonnées sont exprimées dans un espace à 3 dimensions. Je détermine assez facilement les coordonnées d'un vecteur normal V(A,B,C) au plan le plus proche de ces points.

J'ai besoin de faire une projection des points sur le plan définit par V et par un point arbitraire (origine par exemple) et d'exprimer les coordonnées de chaque points projetés en 2D (relatifs au plan).

Je ne sais pas vraiment comment m'y prendre.

Merci pour votre aide

Julien

[abel]

On m'avait posé exactement le meme pb il y a qques temps.

http://www.maths-forum.com/showthread.php?t=14654

[Daragon geoffrey]

slt
on note M(x;y;z) n'appartenant pas à (ABC), alors on pose D son projeté orthogonal sur (ABC), de plus on a vecteur MD et n (vecteur normal à (ABC)) colinéaires équiv à il existe k réel tel que MD=k*n, tu détermines ainsi un système d'équations paramétriques de la droite (MD), or D vérifie également l'équation de (ABC), tu remplaces alors ds cette équation pour déterminer la valeur du paramètre t intervanant ds la représentation paramétrique de (MD), tu en déduis ainsi les coordonnées de D et pour terminer, ds la base vectorielle (a;AB;AC) tu cherches x et y réels tels que AD=x*AB + y*AC par passage aux coordonnées ! x et y représentent les coordonnées de D ds la reère vectoriel 2D ! idem avec les autres points ! @ +

[abel]

Je trouve qu'il est + simple de changer de repère (avec une base qui contient V/||V|| et dont l'origine est le point arbitraire), comme ça, projeter un point revient à lui retirer sa coordonnées sur V, ensuite il reste plus qu'à se remettre dans l'ancien repère (en utilisant des matrices de passage et des translations).

[Daragon geoffrey]

je te fait confiance abel parcequ'à vrai dire je n'ai pas encore eu l'occasion d'apprendre les matrices de rotation ds mon cursus scolaire ! @ +

[abel]

T'inquiète pas ça viendra.... :mur:
Mais ca veut pas dire que ta méthode ne marche pas.

[timoch]

Merci bien pour les réponses.

Je vais résumer ce que j'ai compris histoire d'être sûr que j'ai effectivement compris :

Soit un vecteur de norme 1,
Soit un point,
Soit le plan défini par V et P,
Soit un point à projeter sur selon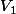

Je crée arbitrairement un vecteur de norme 1 et je calcule résultat du produit vectoriel entre 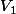et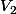

Je crée la matrice de passage M de la base des vecteurs unitaires vers la base des vecteurs :

Pour obtenir les coordonnées de dans la base , je calcule

J'obtiens les coordonnées du projeté de dans le repère du plan en enlevant la première coordonnée de .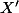

J'espère avoir bien compris. J'ai un doute au moment du changement de base (est-ce que je dois prendre la transposée de M ?).

Merci pour l'aide

Julien

[Amine.MASS]

Pour obtenir les coordonnées de dans la base , je calcule

bonjour,

Je crée arbitrairement un vecteur

doit étre orthogonal a
sinon le reste me semble juste
cordialement,Amine