Exercice approfondissement : Lycée 1ereS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 05 Déc 2011, 19:59
par Alano-o » 05 Déc 2011, 19:59
On considère la courbe

d'équation y=;)x et la courbe

' d'équation y=x² sur[0;+;)[.
La droite d a pour équation y=x.
1 Soit les points M(a;b) et N(b;a) où a et b sont deux réels.
a.Démontrer que OM=ON.
[CENTER]Pour a et b

0
OM=
;)((a-0)²+(b-0)²)=;)((a²+b²)ON=
;)((b-0)²+(a-0)²)=;)((b²+a²);)((b²+a²)=;)((a²+b²)?[/CENTER]
[RIGHT]Donc OM=ON[/RIGHT]
b. Démontrer que le milieu de [MN]

d
[CENTER] Milieu : I I de M =

(x_n-x_m )/2 +

(x_m-x_n )/2
(_(...) Indice)[/CENTER]
JE bloque ici :/ merci de m'aider

svp
(j'ai une idée pour la suite mais bon j'attends de voir )
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 05 Déc 2011, 20:57
par el niala » 05 Déc 2011, 20:57
ce n'est pas très lisible :doh:
1a) ça a l'air correct
1b) pas clair du tout, le milieu d'un segment a pour coordonnées la demi-somme des coordonnées des extrémités du segment, d'où celles de I, ne remarques-tu pas
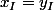
par hasard ?
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 19:27
par Alano-o » 08 Déc 2011, 19:27
el niala a écrit:ce n'est pas très lisible :doh:
1a) ça a l'air correct
1b) pas clair du tout, le milieu d'un segment a pour coordonnées la demi-somme des coordonnées des extrémités du segment, d'où celles de I, ne remarques-tu pas
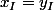
par hasard ?
Je crois avoir trouvé, j'envoie ce que j'ai trouvé

PS : effectivement mon 1B je vois pas pourquoi j'ai fais sa, ça n'a aucun sens ^^'
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 19:35
par Alano-o » 08 Déc 2011, 19:35
1b) on a

I milieu de [MN] :

=
/2)
=
/2)

=
/2)
=
/2)
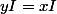
donc I appartient à d :we:
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 19:44
par Alano-o » 08 Déc 2011, 19:44
c)
En déduire que M et N sont symétriques par rapport à d Comme :
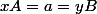
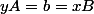
I appartient à d
alors A est symétrique à B par rapport à d.
2)
Soit M le point d'abscisse a de 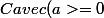)
2)a
Quelles sont les coordonnées de M?Comme
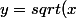)
et
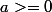
alors le point M d'abscisse "a" a pour ordonnée
)
))
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 19:51
par Alano-o » 08 Déc 2011, 19:51
2)
b
Démontrez que son symétrique M' par rapport à d appartient a 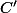
On a
))
et
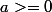
et
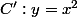
pour que M' soit le symétrique de M :
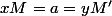
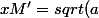=yM)
et on a
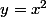
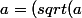^2)
Donc
;a))
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 08 Déc 2011, 19:53
par el niala » 08 Déc 2011, 19:53
1c) non, ta démonstration est incomplète, ce n'est pas parce le milieu d'un segment est sur un droite que ses extrémités sont symétriques par rapport à cette droite, tu as oublié d'utiliser 1a)
2a) OK
détail : pour

tape \ge (pour greater or equal)
2b) c'est un peu maladroit je trouve, explique simplement que le symétrique de M a pour coordonnées
)
et que ces coordonnées vérifient l'équation de C'
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 20:06
par Alano-o » 08 Déc 2011, 20:06
:stupid_in
2)
c
Réciproquement, soit N un point de  . Démontrer que son symétrique N' par rapport à d appartient à C.
. Démontrer que son symétrique N' par rapport à d appartient à C.
On a
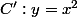
et
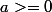
Soit
)
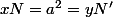
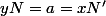
pour que N' soit le symétrique de N par rapport d
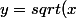)
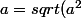)
Je suis un peu pommé ^^
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 20:07
par Alano-o » 08 Déc 2011, 20:07
el niala a écrit:1c) non, ta démonstration est incomplète, ce n'est pas parce le milieu d'un segment est sur un droite que ses extrémités sont symétriques par rapport à cette droite, tu as oublié d'utiliser 1a)
2a) OK
détail : pour

tape \ge (pour greater or equal)
2b) c'est un peu maladroit je trouve, explique simplement que le symétrique de M a pour coordonnées
)
et que ces coordonnées vérifient l'équation de C'
Je retiens

-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 08 Déc 2011, 20:24
par el niala » 08 Déc 2011, 20:24
Je suis un peu pommé
ça, je ne sais pas, "paumé" peut-être un peu
si tu poses N(a²,a) tu ne risques pas d'y arriver :triste:
essaie plutôt N(a,a²) d'où son symétrique N'(a²,a) et tu devrais pouvoir conclure...
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 20:43
par Alano-o » 08 Déc 2011, 20:43
el niala a écrit:Je suis un peu pommé
ça, je ne sais pas, "paumé" peut-être un peu
si tu poses N(a²,a) tu ne risques pas d'y arriver :triste:
essaie plutôt N(a,a²) d'où son symétrique N'(a²,a) et tu devrais pouvoir conclure...
Ah oui !
Mais pour le le 1)c je n'ai pas compris ce que je devais faire enfaite.. Utiliser 1)a? Comment ça?
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 20:45
par Alano-o » 08 Déc 2011, 20:45
Alano-o a écrit::stupid_in
2)
c
Réciproquement, soit N un point de 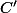 . Démontrer que son symétrique N' par rapport à d appartient à C.
. Démontrer que son symétrique N' par rapport à d appartient à C.
On a
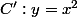
et
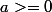
Soit
)
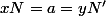
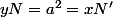
pour que N' soit le symétrique de N par rapport d
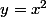
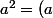2)
Je suis un peu "paumé" ^^
Comme cela?
et donc on a
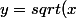)
donc
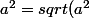)
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 08 Déc 2011, 20:55
par el niala » 08 Déc 2011, 20:55
ne multiplie pas les posts, sinon, ça va vite devenir capharnaum !
pour 1c) tu as montré que le milieu de M(a,b) et N(b,a) était sur d, et tu conclus (abusivement) que N est le symétrique de M par rapport à d
il existe une infinité de droites qui passent par I, pour autant il n'y en a qu'une qui est axe de symétrie pour [MN]
tu ne vois pas en quoi le résultat de 1a) peut t'aider ?
pour 2) c'est une simple application des résultats précédents
N(a,a²) est sur C', N'(a²,a) est son symétrique par rapport à d (cf 1c) or si tu poses b=a², tu montres aussitôt que N' est sur C, cqfd (ou qed si tu préfères le latin)
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 20:58
par Alano-o » 08 Déc 2011, 20:58
el niala a écrit:ne multiplie pas les posts, sinon, ça va vite devenir capharnaum !
pour 1c) tu as montré que le milieu de M(a,b) et N(b,a) était sur d, et tu conclus (abusivement) que N est le symétrique de M par rapport à d
il existe une infinité de droites qui passent par I, pour autant il n'y en a qu'une qui est axe de symétrie pour [MN]
tu ne vois pas en quoi le résultat de 1a) peut t'aider ?
pour 2) c'est une simple application des résultats précédents
N(a,a²) est sur C', N'(a²,a) est son symétrique par rapport à d (cf 1c) or si tu poses b=a², tu montres aussitôt que N' est sur C, cqfd (ou qed si tu préfères le latin)
Je vois pas :/
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 08 Déc 2011, 21:01
par el niala » 08 Déc 2011, 21:01
essaie d'être un peu plus disert, que ne vois-tu pas :
- la pertinence de ma remarque ?
- l'utilisation de 1a) ?
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 21:02
par Alano-o » 08 Déc 2011, 21:02
Ah si ! je crois comprendre mais cela veut dire qu'on admet que C' et C sont symétriques ..?
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 08 Déc 2011, 21:07
par Alano-o » 08 Déc 2011, 21:07
Je ne comprend pas l'utilite de la 1)a
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 08 Déc 2011, 21:21
par el niala » 08 Déc 2011, 21:21
considère le triangle MON,
pour que d - ie (OI) - soit axe de symétrie pour [MN], le fait que ce soit une médiane suffit-il ?
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 09 Déc 2011, 19:01
par Alano-o » 09 Déc 2011, 19:01
el niala a écrit:considère le triangle MON,
pour que d - ie (OI) - soit axe de symétrie pour [MN], le fait que ce soit une médiane suffit-il ?
J'ai trouver pour les symétriques !

je te montre sa
-
Alano-o
- Membre Naturel
- Messages: 19
- Enregistré le: 17 Oct 2011, 18:25
-
 par Alano-o » 09 Déc 2011, 19:15
par Alano-o » 09 Déc 2011, 19:15
pour a=bLes point M et N sont donc confondus. Et donc appartiennent à d. Ainsi M et N sont symétriques à d.
pour 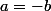
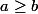
I le milieu [MN] est confondu a O ( du repère)
M et N appartiennent donc a
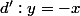
. la droite d' est perpendiculaire a
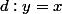
donc [MN] est perpendiculaire a d. Ainsi M est symétrique à N par rapport à d
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
