Terminale: nombres complexes

[Madlord]

Bounjour,

Je suis actuellement bloqué sur un exercice sur les complexes et je solicite votre aide, l'exercice est le suivant :

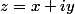
On a un nombre et

On cherche à montrer que l'essemble des points M invariants par la transformation qui transforme z en z' est une droite D d'équation

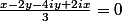
Alors j'ai fait l'équation z=z' et je tombe sur , je pense qu'on est loin du résutat attendu, y'a-t-il une autre methode pour arriver à trouvher l'équation de cette droite ?

[Sa Majesté]

Salut

Tu es au contraire très proche du résultat
Un nombre complexe est nul ssi sa partie réelle et sa partie imaginaire sont nulles

[Madlord]

Merci à toi j'ai eu du mal à comprendre là où tu voulais en venir mais c'est à cause d'erreurs de calcul ... Une fois cette "difficulté" surmontée j'ai réussi mon exercie.

[Shmineu]

Bonjour j'ai besoin d'aide pour cet exercice svp: (O,u,v) est un repère orthonorme du plan complexe. On considère les points B et C d'affixes respectives b=1-i et c=2+2i . On considère les points B' et C' tels que les triangles OB'B et OCC' soient rectangles isocèles de sommet O et de sens direct. 1) Déterminer les affixes b' et c' des points B' et C'. 2) K est le milieu de[BC] d'affixe k. Calculer c'-b'/k. En déduire une mesure de l'angle de vecteurs (OK,B'C') et la valeur du rapport B'C'/OK. 3) Soit f la transformation du plan qui, à tout point M d'affixe z, associe le point M' d'affixe z'=2iz-1-i. A) Déterminer les images des points O et K par f. B) Montrer que, quels soient les points M et N distincts et leur images M' et N' par f, on a : ZM'-ZN'/ZM-ZN=2i. 4a) Montrer que la transformation f admet un seul point invariant A dont on déterminera son affixe a. Placer A sur la figure. B) Montrer que (AM,AM')=pi/2[2pi] et que AM'=2AM. 5) Soit h l'homothetie de centre B de rapport 2 et r la rotation de centre O d'angle pi/2. Montrer, en utilisant les écritures complexes de h et r,que f=r o h. J'ai besoin de votre aide svp je suis bloque a la question 3b). Merci d'avance