Bonsoir,
Pourrait-on m'aider à trouver la forme canonique de : -8x²+6x+5 ?
Je suis resté à cette réponse : -2(2x-3/4)²+49/8 , quand je la développe , ça retombe bien sur -8x²+6x+5 mais il ne devrait avoir qu'un x... cela se confirme lorsque je cherche l'extremum de f sur R, je ne trouve pas les bonnes valeurs... :hum:
Merci d'avance !
Forme canonique
9 messages
- Page 1 sur 1
kikou8 a écrit:Bonsoir,
Pourrait-on m'aider à trouver la forme canonique de : 8x²+6x+5 ?
Je suis resté à cette réponse : -2(2x-3/4) + 49/8 , quand je la développe , ça retombe bien sur 8x²+6x+5 mais il ne devrait avoir qu'un x... cela se confirme lorsque je cherche l'extremum de f sur R, je ne trouve pas les bonnes valeurs... :hum:
Merci d'avance !
salutt, commen, tu as trouver ca, alors qu'une forme canonique on devrais avoir a(x-A)²+B
kikou8 a écrit:Bonsoir,
Pourrait-on m'aider à trouver la forme canonique de : 8x²+6x+5 ?
Je suis resté à cette réponse : -2(2x-3/4) + 49/8 , quand je la développe , ça retombe bien sur 8x²+6x+5 mais il ne devrait avoir qu'un x... cela se confirme lorsque je cherche l'extremum de f sur R, je ne trouve pas les bonnes valeurs... :hum:
Merci d'avance !
Je suppose que tu as voulu écrire : -2(2x-3/4)² + 49/8
Mais même ainsi, il y a un os quelque part.
-2(2x-3/4)² + 49/8 est égal à -8x²+6x+5 et pas à 8x²+6x+5 comme tu l'as écrit.
:zen:
kikou8 a écrit:Bonsoir,
Pourrait-on m'aider à trouver la forme canonique de : 8x²+6x+5 ?
Je suis resté à cette réponse : -2(2x-3/4)+ 49/8 , quand je la développe , ça retombe bien sur 8x²+6x+5 mais il ne devrait avoir qu'un x... cela se confirme lorsque je cherche l'extremum de f sur R, je ne trouve pas les bonnes valeurs... :hum:
Merci d'avance !
Pardon je rectifie :
La forme canonique est : -8x²+6x+5 , et j'ai trouvé -2(2x-3/4)²+49/8 .
Mais quelqu'un aurait-il trouvé la réponse, car je n'arrive vraiment pas...
Ni l'un ni l'autre.
La forme canonique de - est -
est -^2+\frac{49}{8}) .
.
Ce résultat est donné en guise de vérification de vos résultats, mais vous ne pouvez pas marquer ça directement dans une copie.
Pour trouver cette forme canonique, il y a une méthode calculatoire, celle que j'utilise, et une méthode par formule, que l'on vous enseigne.
Dans votre cours vous avez vu que la forme canonique de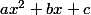 est
est +\beta) où
où 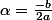 et
et  .
.  est l'abscisse du sommet de la parabole et
est l'abscisse du sommet de la parabole et  son ordonnée.
son ordonnée.
En résumé la forme canonique de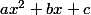 est
est ^2+[\frac{ab^2}{4a^2}-\frac{b^2}{2a}+c]) .
.
Bon courage !
La forme canonique de -
Ce résultat est donné en guise de vérification de vos résultats, mais vous ne pouvez pas marquer ça directement dans une copie.
Pour trouver cette forme canonique, il y a une méthode calculatoire, celle que j'utilise, et une méthode par formule, que l'on vous enseigne.
Dans votre cours vous avez vu que la forme canonique de
En résumé la forme canonique de
Bon courage !
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
