Barycentres.

[Grugh]

Bonsoir, voila j'ai un petit soucis pour terminer mon exercice :cry: , pourriez vous m'aider svp? Vioci l'énoncé:
ABC est un triangle avec A(-3,0),B(-1,5) et C(4,3).
1°) Il faut faire la figure et placer G le centre de gravité et I le milieu de [AC], aprés avoir trouvé leurs coordonnées.
2°) Quelle est la nature de ABC.
3°) Démontrer que tous les point M su plan tel que : (norme des vecteurs) MA+MB+MC= 3/2 (normes des vecteurs) MA+MC, est une doite dont on trouvera les caractéristiques.
4°) Déterminer un vecteur directeur de cette droite (justifier et donner les coordonnées).
5°)Déterminer une équation cartésienne.

Voila je trouve ceci:
1°) xG= 0et yG=8/3
xI=0.5 etyI=1.5
2°)J'arrive à isocèle rectangle en B aprés plusieurs calculs.
3°) J'arrive à M appartient à la médiatrice [IG]

Voila pour la 3, je ne sais pas quoi dire pour "trouvera les caractéristiques"., et je bloque pour les 2 dernières. Merci d'avance pour votre aide.

[Grugh]

Up svp (désolé d'être si préssé).

[Sh0nty]

Bonsoir Grugh,

Les caractéristiques d'une droite c'est, par exemple : médiatrice de [..], hauteur issue de . dans le triangle ..., etc...

Pour la suite, tu tois t'aider de la question 3)...

Sh0nty

[Arnaud-29-31]

Salut,

C'est correct pour les questions 1 et 2,
Les points M décrivent bien la médiatrice de [IG] ... les caractéristiques d'une médiatrice je pense que tu connais ... par où elle passe, elle vérifie quoi etc ... ?

Pour la suite si je te demande d'abord un vecteur normal puis ensuite un vecteur directeur, est-ce que ca t'aide ?

[Grugh]

Merci à vous deux pour votre réponse. Non, je n'arrive même pas à donner un autre vecteur afin de donner un vecteur directeur aprés, je suis vraiment bloqué la dessus :mur: . Les caractéristiques sont que tous les points de la médiatrice sont à la même distance des deux extrémités.

[Arnaud-29-31]

Oui et aussi elle passe par un point caractéristique du segment [IG] et elle coupe ce segment [IG] d'une certaine manière ...

[Grugh]

Oui et aussi elle passe par un point caractéristique du segment [IG] et elle coupe ce segment [IG] d'une certaine manière ...

Oui par son milieu. Par contre pour la 4, je ne vois vraiment pas comment on peut faire :mur:

[Arnaud-29-31]

Bein comme je t'ai dit, donne d'abord un vecteur normal.

[Grugh]

Bah je ne vois pas du tout, peut être le milieu de [IG] que j'appelle k donc KC?

[Arnaud-29-31]

On a une droite perpendiculaire à [IG] ... et on veut un vecteur normal à cette droite ... je vois pas ce qui te bloque, il y'a un vecteur normal évident la.

[Grugh]

Ah je vois ce que tu veux dire, mais je ne vois pas comment je peux le traduire. ( j'ai des gros soucis avec les vecteurs comme tu le constate ).

[Arnaud-29-31]

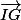
Tu es d'accord que le vecteur est normal à la médiatrice de [IG] ? ...

[Grugh]

Oui donc le vecteur normal de la médiatrice serait le milieu de [IG] à un autre point de la médiatrice?

[Arnaud-29-31]

Non ca ca donne un vecteur directeur.
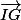
Mais on sait que est vecteur normal. On peut le déterminer puisqu'on connaît les coordonnées de I et de G. Et si on a un vecteur normal, on a de manière immédiate un vecteur directeur.

[Grugh]

Oui mais c'est bien le vecteur directeur de la médiatrice qu'il faut donner non?

[Arnaud-29-31]

Bein oui, je viens de te dire qu'on peut le déduire de manière immédiate une fois que l'on a exprimé le vecteur normal.

[Grugh]

coordonnéesdu de IG: -1/2; 7/6.

[Arnaud-29-31]

Oui voila, est un vecteur normal.
On peut arranger les coefficients et écrire

[Grugh]

Ah, je ne pensais pas à cela, et j'étais vraiment à côté, et c'est à partir de cela comment peut-on definir un vecteur directeur de la médiatrice?

[Arnaud-29-31]

Et bein le vecteur directeur est normal au vecteur normal ...