Bonjour, voila, j'ai un Dm de mathématiques en 1ère S . Je coince pour la dernière question et je voudrais que vous me corrigez les questions 1,2,3.
Sujet:
I)
1. On considère l'équation du second degré ax²+bx+c= 0. Dans le cas où elle possède deux solutions distinctes, écrire la somme S et le produit P de ses deux racines en fonction de a,b,c.
2. Même question si l'équation possède une solution double.
3. On connaît la somme S et le produit P de deux nombres a et b. Montrer, en cherchant à résoudre le système d'inconnues{a+b=S que les nombres a et
ab=P
sont les solutions, si elles existent de l'équation x²-Sx+P=0.
4. Application: Trouver deux nombres dont la somme est 10 et le produit 12.75
II) 1.a déterminer un polynôme P du second degré tel que l'on ait, pour tout réel x:
P(x+1)-P(x)=x
b écrire l'égalité précédente pour x=1, x=2, ..., x=n
c en déduire la somme S1=1+2+...+n
:mur: que je n'ai absolument pas compris. Même pas la question 1.
Problème de mathématique 1èreS
9 messages
- Page 1 sur 1
voici ce que j'ai trouvé:
1)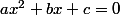

Admettons que . On a donc deux racines distinctes:
. On a donc deux racines distinctes:

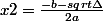
Somme de deux racines: +
+ =
= 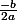
Donc S=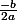
Produit des deux racines:


= Le tout
Le tout ( je sais pas comment mettre des parenthèse a une fraction à droite.)
( je sais pas comment mettre des parenthèse a une fraction à droite.)
=
=}{4a^2})
=
= =
= 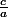
Donc P=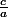
2) Admettons que =0. On a donc une racine double:
=0. On a donc une racine double:
S =
=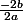
=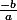
P =
=
3)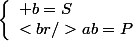
=P<br />\end{array}<br />\right.)
b(S-b)=P
 bs-b
bs-b =P
=P
 bs=P+b
bs=P+b
 0=P+b
0=P+b
 b
b +P-sb=0
+P-sb=0
On peut remplacer b par x a et b sont considéré les solution: x +P-Sx
+P-Sx
x -Sx+P
-Sx+P
Donc voila tout ce que j'ai trouvé.( j'ai mis énormément de temps pour tout marqué des jolies formules rien que pour le correcteur. Et ce ne fut pas évident pour moi au début) Merci de votre compréhension
1)
Admettons que
Somme de deux racines:
Donc S=
Produit des deux racines:
=
=
=
=
=
Donc P=
2) Admettons que
S =
=
=
P =
=
3)
b(S-b)=P
On peut remplacer b par x a et b sont considéré les solution: x
x
Donc voila tout ce que j'ai trouvé.( j'ai mis énormément de temps pour tout marqué des jolies formules rien que pour le correcteur. Et ce ne fut pas évident pour moi au début) Merci de votre compréhension
Les-simpsons a écrit:
Produit des deux racines:
=Le tout
( je sais pas comment mettre des parenthèse a une fraction à droite.)
comme ceci :
?
Les trois premières sont justes (et merci d'avoir utiliser les balises TEX, c'est quand même beaucoup plus lisible).
Ensuite pour P(x+1)-P(x)=x, P est du second degré donc :
donc tu remplaces P(x+1) et P(x) dans l'expression, tu développes le terme de gauche, et tu identifies les coefficients avec le terme de droite.
Les-simpsons a écrit:Et j'ai pas compris comment on fait pour l'exercice n°2 petit 1a?
Tu supposes que
tu développes, tu réduis, et tu utilises la propriété "si un polynôme est nul pour tout x réel, alors ce polynôme a ses coefficients tous nuls".
tu vas trouver a et b ; pour c tu dois utiliser la condition P(0)=0.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
