Endomorphisme de M2(IR)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 13 Sep 2010, 21:48
par MacManus » 13 Sep 2010, 21:48
Bonsoir.
Soit M une matrice de
)
, par exemple : M =

, où a, b, c et d sont des coefficients réels.
On peut exprimer M dans la "base canonique" de
)
qui est
)
.
On a donc M =

-
lucky_star
- Messages: 6
- Enregistré le: 13 Sep 2010, 21:00
-
 par lucky_star » 14 Sep 2010, 17:15
par lucky_star » 14 Sep 2010, 17:15
Bonjour,
la matrice de fA dans la base canonique de
\( \array{a&0&b&0\\0&a&0&b\\c&0&d&0\\0&c&0&d}\)) Déterminer le rang de fA en fonction de celui de A.
Déterminer le rang de fA en fonction de celui de A.J'avoue ne toujours pas savoir comment calculer le rang d'une matrice... :dodo:
à part avec le pivot de gauss, qui permet d'avoir une matrice échelonnée.
Une idée s'il vous plait?
Merci beaucoup

-
lucky_star
- Messages: 6
- Enregistré le: 13 Sep 2010, 21:00
-
 par lucky_star » 14 Sep 2010, 17:58
par lucky_star » 14 Sep 2010, 17:58
Bonjour,
la matrice de fA dans la base canonique de
\( \array{a&0&b&0\\0&a&0&b\\c&0&d&0\\0&c&0&d}\)) Déterminer le rang de fA en fonction de celui de A.
Déterminer le rang de fA en fonction de celui de A.J'avoue ne toujours pas savoir comment calculer le rang d'une matrice... :dodo:
à part avec le pivot de gauss, qui permet d'avoir une matrice échelonnée.
Une idée s'il vous plait?
Merci beaucoup

-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 14 Sep 2010, 18:13
par MacManus » 14 Sep 2010, 18:13
Et bien tu peux regarder si tes vecteurs colonnes (ou lignes) sont linéairement indépendants : le rang d'une matrice peut être calculé comme étant le nombre maximal de vecteurs linéairement indépendants.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 15 Sep 2010, 14:39
par Doraki » 15 Sep 2010, 14:39
Non, c'est juste.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 15 Sep 2010, 15:10
par mehdi-128 » 15 Sep 2010, 15:10
Jéjouille a écrit:Heu, ça n'appartient pas à M2(R) ??
Je dois faire une belle confusion !
)=4)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 15 Sep 2010, 15:13
par mehdi-128 » 15 Sep 2010, 15:13
lucky_star a écrit: qui a toute matrice M associe AM. \\<br />Quelle est la matrice f_A dans la base canonique de M_2(IR)?\\<br />Determiner le rang de f_A en fonction de celui de A.\\<br /> \\<br /> \\<br />\textit{Quelle est la matrice f_A dans la base canonique de M_2(IR)}?\\Je suis bloque'\\qu'est ce que la base canonique de M_2(IR)?\\Merci et bonne soiree)
Que vaut A ?
-
lucky_star
- Messages: 6
- Enregistré le: 13 Sep 2010, 21:00
-
 par lucky_star » 15 Sep 2010, 17:29
par lucky_star » 15 Sep 2010, 17:29
A=
)
fA =
)
soit
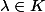
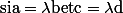
alors le rang de f(A)=2 et le rang de A=1
si

alors le rang de f(A)=4 et le rang de A=2
est-ce ce qu'il faut faire?
Merci
-
lucky_star
- Messages: 6
- Enregistré le: 13 Sep 2010, 21:00
-
 par lucky_star » 15 Sep 2010, 17:57
par lucky_star » 15 Sep 2010, 17:57
A=
)
fA =
)
soit
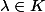
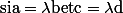
alors le rang de f(A)=2 et le rang de A=1
si

alors le rang de f(A)=4 et le rang de A=2
est-ce ce qu'il faut faire?
Merci
-
lucky_star
- Messages: 6
- Enregistré le: 13 Sep 2010, 21:00
-
 par lucky_star » 15 Sep 2010, 18:39
par lucky_star » 15 Sep 2010, 18:39
A=
)
fA =
)
soit
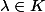
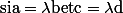
alors le rang de f(A)=2 et le rang de A=1
si

alors le rang de f(A)=4 et le rang de A=2
est-ce ce qu'il faut faire?
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
