Bonjour
J'aimerais avoir une démonstration rigoureuse de l'algorithme de la division euclidienne qu'on apprend au primaire. Si quelqu'un a ça se serait super. Merci d'avance...
Division euclidienne
11 messages
- Page 1 sur 1
Je pense que tu veux parler de l'algorithme d'Euclide.
Va voir ici : http://fr.wikipedia.org/wiki/Algorithme_d'Euclide
Va voir ici : http://fr.wikipedia.org/wiki/Algorithme_d'Euclide
Dinozzo13 a écrit:Salut !
C'est la définition de la division euclidienne ou l'algorithme d'Euclide que tu veux ?
Merci pour ta réponse, mais je ne voulais pas parler de l'algorithme d'Euclide qui permet de trouver le PGCD mais plutot de l'explication permettant de justifier la mécanique de notre division dite euclidienne. Merci
L'algorithme utilise le principe que pour calculer la division de x = (10a+b) par d,
on fait d'abord la division de a par d (récursivement) :
On obtient a = dq+r, avec 0<=r
Ensuite on fait la division euclidienne de 10r+b, qui est un "petit" nombre donc on la fait à la main :
r <= d-1 et b < 10 donc 10r+d < 10(d-1)+10 = 10d : le quotient est un nombre entre 0 et 9, et on écrit (10r+b) = q'd + r'.
On a alors que x = (10q+q')*d + r', avec 0 <= r' < d, ce qui est la forme souhaitée. 10q+q' est donc le quotient et r' est le reste.
on fait d'abord la division de a par d (récursivement) :
On obtient a = dq+r, avec 0<=r
Ensuite on fait la division euclidienne de 10r+b, qui est un "petit" nombre donc on la fait à la main :
r <= d-1 et b < 10 donc 10r+d < 10(d-1)+10 = 10d : le quotient est un nombre entre 0 et 9, et on écrit (10r+b) = q'd + r'.
On a alors que x = (10q+q')*d + r', avec 0 <= r' < d, ce qui est la forme souhaitée. 10q+q' est donc le quotient et r' est le reste.
Le plus grand commun diviseur ou PGCD d'entiers naturels est le plus grand diviseur commun à ces entiers naturels.
Le PGCD de deux entiers a et b est noté :) ou encore
ou encore 
Propriété :
Si l'on décompose des entiers naturels en produits de facteurs premiers, leur PGCD est le produit de tous les facteurs premier communs à toutes les décompositions affectés du plus petit exposant.
Exemple :



Donc .
.
On peut aussi rechercher le PGCD grace à l'algorithme d'Euclide :
Soit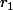 le reste de la division de
le reste de la division de  par
par 
) ;
;
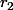 le reste de la division de
le reste de la division de  par
par 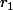 ;
;
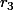 le reste de la division de
le reste de la division de 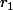 par
par 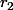 ;
;
...
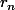 le reste de la division de
le reste de la division de  par
par 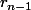 .
.
On a alors :
=a\wedge b=b\wedge r_1=r_1 \wedge r_2 =...=r_{n-1} \wedge r_n = r_n \wedge 0 = r_n) .
.
en désignant le dernier reste non nul.
le dernier reste non nul.
Exemple :
Cherchons le PGCD des nombres a = 3 206 et b=847.
La disposition pratique est la suivante :
http://img821.imageshack.us/img821/3232/pgcd.jpg
Donc .
.
Voilà, en espérant t'avoir aidé ^^
Le PGCD de deux entiers a et b est noté :
Propriété :
Si l'on décompose des entiers naturels en produits de facteurs premiers, leur PGCD est le produit de tous les facteurs premier communs à toutes les décompositions affectés du plus petit exposant.
Exemple :
Donc
On peut aussi rechercher le PGCD grace à l'algorithme d'Euclide :
Soit
...
On a alors :
en désignant
Exemple :
Cherchons le PGCD des nombres a = 3 206 et b=847.
La disposition pratique est la suivante :
http://img821.imageshack.us/img821/3232/pgcd.jpg
Donc
Voilà, en espérant t'avoir aidé ^^
Ben une fois que tu poses les calculs et que tu intuites ce que l'algo est supposé faire, ce n'est plus très dur de vérifier que en effet ça fait bien ce qu'il faut. (enfin bon pour moi aussi c'était pas trivial en cm2, un algorithme c'est un truc un peu détaché du reste, et l'étude d'un algo n'est pas forcément quelquechose qui vient très naturellement, en plus c'est jamais simple à formaliser)
Doraki a écrit:Ben une fois que tu poses les calculs et que tu intuites ce que l'algo est supposé faire, ce n'est plus très dur de vérifier que en effet ça fait bien ce qu'il faut. (enfin bon pour moi aussi c'était pas trivial en cm2, un algorithme c'est un truc un peu détaché du reste, et l'étude d'un algo n'est pas forcément quelquechose qui vient très naturellement, en plus c'est jamais simple à formaliser)
En effet.
Merci encore. A+
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
