Asymptotes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Irish coffee
- Membre Naturel
- Messages: 32
- Enregistré le: 27 Mai 2010, 09:33
-
 par Irish coffee » 16 Juil 2010, 23:30
par Irish coffee » 16 Juil 2010, 23:30
Bonjour à tous, dans un exercice il me demande de démontrer que f(x)=(x²+3)/(x-1) , admet deux asymptotes
???????????
merci de m'aider
-
lol37
- Membre Relatif
- Messages: 139
- Enregistré le: 17 Avr 2010, 13:39
-
 par lol37 » 16 Juil 2010, 23:38
par lol37 » 16 Juil 2010, 23:38
Salut,
tu vois que la fonction n'est pas définie sur 1 ( division par 0 sinon ) -> tu as une asymptote verticale
puis tu détermines les limites vers l'infini et tu conclus.
il y a une asymptote oblique d'équation

tu dois déterminer a et b :
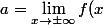 \over x)
et
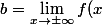-ax})
-
Black Jack
 par Black Jack » 17 Juil 2010, 10:16
par Black Jack » 17 Juil 2010, 10:16
Ou bien ainsi:
f(x)=(x²+3)/(x-1)
f(x) = x + 1 + 4/(x-1)
Ecrit sous cette forme, les 2 asymptotes (l'une verticale et l'autre oblique) sont immédiates à trouver.
:zen:
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 17 Juil 2010, 11:18
par oscar » 17 Juil 2010, 11:18
Asymptotes
verticale x=1 anuule le dénominateur
Oblique le degre du numérateur = degré du numérayteur +1
y =ax +b Calculer a et b par identification
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 137 invités
