équation différentielle de second ordre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Solofein
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2010, 16:15
-
 par Solofein » 05 Avr 2010, 13:44
par Solofein » 05 Avr 2010, 13:44
Bonjour,
Je cherche à résoudre l'équation différentielle d'ordre 2 suivante :
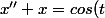)
Pour la résolution sans second membre pas de problème, j'étudie le polynôme caractéristique ...
Mais pour trouver l'ensemble des solutions générales je galère un peu ...
J'ai cherché un
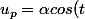 + \beta sin(t))
tel que
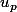
soit solution de l'équa diff mais sans résultats concluant ...
Suis-je obligé d'utiliser la méthode de variation de la constante dans ce cas ?
Merci d'avance.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Avr 2010, 13:55
par barbu23 » 05 Avr 2010, 13:55
tu remplaces
 = \alpha \cos (t) + \beta \sin (t) $)
dans
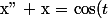 $)
et ensuite tu te trouveras devant un petit système d'equations à resoudre pour trouver les valeurs de

et

.
:happy3:
-
Solofein
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2010, 16:15
-
 par Solofein » 05 Avr 2010, 14:09
par Solofein » 05 Avr 2010, 14:09
barbu23 a écrit:tu remplaces
 = \alpha \cos (t) + \beta \sin (t) $)
dans
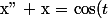 $)
et ensuite tu te trouveras devant un petit système d'equations à resoudre pour trouver les valeurs de

et

.
:happy3:
Bonjour,
Bah en posant
=\alpha cos(t) + \beta sin(t))
on a :
=- \alpha cos(t) - \beta sin(t))
Je remplace tout ça dans ma superbe équation et j'obtiens
 cos(t) + (\beta - \beta) sin(t) = cos(t))
...
Enfin j'ai ptetre fait des erreurs de calcule/raisonnement mais j'ai pas l'impression que ce soit concluant ...
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 05 Avr 2010, 14:27
par Finrod » 05 Avr 2010, 14:27
ça fait bien zéro.
C'est une solution de l'équation sans second membre.
essai (1/2)t sin(t)
-
Solofein
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2010, 16:15
-
 par Solofein » 05 Avr 2010, 14:40
par Solofein » 05 Avr 2010, 14:40
Finrod a écrit:ça fait bien zéro.
C'est une solution de l'équation sans second membre.
essai (1/2)t sin(t)
Okay,
donc avec
 = \frac{1}{2} t sin(t))
j'obtiens
 = \frac{1}{2} ( 2 cos(t) - t sin(t) ))
Et donc
 + f(t) = cos(t))
...
La solution particulière marche, merci.
Mais comment procéder pour trouver cette solution particulière ? variation de la constante ?
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 05 Avr 2010, 14:45
par prody-G » 05 Avr 2010, 14:45
La forme générale d'une solution de ton équation est :
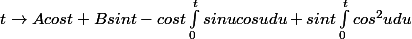
(sauf erreur de calcul)
On peut simplifier le résultat vu que les intégrales se calculent bien.
Avec une variation de la constante tu peux trouver ça.


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Avr 2010, 17:20
par Ben314 » 05 Avr 2010, 17:20
La méthode de prody-G est celle de variation de la constante.
A mon avis, Finrod (qui est un petit malin...) n'a pas procédé comme cela.
Tu as dû trouver que ton équa-diff. homogène x"+x=0 a pour solution les fonctions x(t)=a.cos(t)+b.sin(t) avec a,b réels.
Déja, cela montre que dans l'équation avec second membre x"+x=cos(t), cela ne sert absolument à rien d'essayer x(t)=a.cos(t)+b.sin(t) vu qu'on sait déjà que, dans ce cas, on trouve x"+x=0 !!
La "méthode générale" dit que, dans ce cas là, il faut essayer x(t)=at.cos(t)+bt.sin(t) (i.e. remplacer les constantes par constante.t)
De même, si par exemple cos(t) et t.cos(t) étaient tout les deux solutions de l'équa-diff. homogène et que l'équa-diff. avec second membre contient du cos(t), il faudrait "essayer" x(t)=at².cos(t)+bt².sin(t).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 05 Avr 2010, 17:30
par Finrod » 05 Avr 2010, 17:30
J'ai fait comme toi Ben, en effet. Mes souvenirs n'étaient pas aussi précis.
-
Solofein
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2010, 16:15
-
 par Solofein » 05 Avr 2010, 17:41
par Solofein » 05 Avr 2010, 17:41
Merci beaucoup pour ces explications, je suis moins dans le flou ^_^ la "méthode générale" de changer la constante par constante*t paraît intéréssante et moins risquée niveau erreur de calcul que la variation de la constante ... il faudrait que je m'entraîne à l'utiliser ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
