Groupes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 02 Jan 2010, 16:24
par burton38 » 02 Jan 2010, 16:24
bonjour, voila je bloque sur l'exercice suivant.
G est une groupe de cardinal pq avec p et q premiers tels que pon suppose qu'il existe dans G un element x d'ordre p et un element y d'ordre q. On note H le sous goupe engendré par y.
1)a)Soit K = xHx^-1 = {xhx^-1, hH}
montrer que K est un sous groupe De G de cardinal q
b) montrer que si HK = {e} alors l'application : (h,k) dans HxK ->hk dans G est injective (attention ce n'est pas un morphisme).
c) en deduire que xHx^-1 =H
2) montrer qu'il existe k tel que xyx^-1=y^k avec k=0 mod[q]
3) calculer x^iyx^-i pour tout i dans N
je bloque a la question 3 :marteau: help please
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Jan 2010, 17:29
par yos » 02 Jan 2010, 17:29
burton38 a écrit:2) montrer qu'il existe k tel que xyx^-1=y^k avec k=0 mod[q]
k=0 mod q ??? Relis ton énoncé.
burton38 a écrit:3) calculer x^iyx^-i pour tout i dans N
Regarde pour i=2
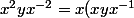x^{-1}=...)
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 02 Jan 2010, 17:45
par burton38 » 02 Jan 2010, 17:45
tu as raison c'est k different 0[q].
merci bien
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 02 Jan 2010, 17:51
par burton38 » 02 Jan 2010, 17:51
je n'arrive pas a monter que K^p=1[q].
une idée ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Jan 2010, 19:14
par yos » 02 Jan 2010, 19:14
burton38 a écrit:je n'arrive pas a monter que K^p=1[q].
une idée ?
C'est une conséquence du résultat de la question 3 lorsque i=p.
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 03 Jan 2010, 09:33
par burton38 » 03 Jan 2010, 09:33
je n'arrive pas a conclure car je ne vois pas comment on introduit la congruence :mur:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Jan 2010, 10:10
par yos » 03 Jan 2010, 10:10
Tu as dû prouver par récurrence que

pour tout entier

.
En particulier

donc

donc
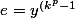})
mais y est d'ordre q donc q divise

.
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 03 Jan 2010, 11:01
par burton38 » 03 Jan 2010, 11:01
tu peut me terminer l'exemple que tu m'a fait pour i=2 stp
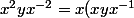x^{-1}=...)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Jan 2010, 11:19
par yos » 03 Jan 2010, 11:19
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 03 Jan 2010, 11:57
par burton38 » 03 Jan 2010, 11:57
que peut-on dire de l'ordre de k(barre) dans le groupe (U(Z/qZ),x) ?
je ne m'en sort pas :(
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 03 Jan 2010, 12:07
par burton38 » 03 Jan 2010, 12:07
c'est bon j'ai trouvé :we:
maintenant si on suppose que k=1[q], comment peut on montrer que g est cyclique ? :hum:
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 03 Jan 2010, 12:31
par burton38 » 03 Jan 2010, 12:31
c bon j'ai trouvé. :we:
mais maintenant si on suppose k=1[q] comment etablir que G est cyclique ? :hum:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Jan 2010, 13:05
par yos » 03 Jan 2010, 13:05
Tu as donc prouvé que xy=yx.
Quel est l'ordre de xy?
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 03 Jan 2010, 13:33
par burton38 » 03 Jan 2010, 13:33
c'est pq donc g est cyclique car il est engendré par xy ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Jan 2010, 13:43
par yos » 03 Jan 2010, 13:43
oui c'est ça.
-
burton38
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Jan 2010, 16:20
-
 par burton38 » 03 Jan 2010, 13:46
par burton38 » 03 Jan 2010, 13:46
mais comment on se sert de k=1[q] ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Jan 2010, 14:22
par yos » 03 Jan 2010, 14:22
k=1+mq montre que

donc que xy=yx.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
