Bonjour,
J'arrive pas à trouver l'erreur que j'ai faite pour déterminer la convergence de cette intégrale:
int [(sint)^a/|lnt|^b] entre 0 et 1/2 avec a et b réel.
Ma solution:
La fonction est continue et positive sur ]0,1/2]. De plus lim (sint)^a/|lnt|^b vaut 0 quand t tend vers 0. On peut donc prolonger par continuité en posant f(0)=0 donc l'intégrale est convergente.
La solution du corrigé:
Ils raisonnent avec les équivalents et cela revient à étudier l'intégrale t^a/|lnt|^b et ensuite ils concluent avec Bertrand.
Merci-
ps: comment on fait pour écrire les symboles mathématiques?
Intégrales généralisées
7 messages
- Page 1 sur 1
Merci j'ai compris...pourtant j'avais vérifié les différents cas :cry:
Par contre j'ai aussi fais une autre méthode dont je ne comprends pas l'erreur.
J'ai majoré le (sint)^a par 1 on a donc : (sint)^a/|lnt|^b < 1/|lnt|^b
puis avec Bertrand et le théorème de comparaison (les fonctions sont bien positives) on conclue que c'est convergent pour tout a,b... je sens que l'erreur vient de la division par ln|t|^b
Par contre j'ai aussi fais une autre méthode dont je ne comprends pas l'erreur.
J'ai majoré le (sint)^a par 1 on a donc : (sint)^a/|lnt|^b < 1/|lnt|^b
puis avec Bertrand et le théorème de comparaison (les fonctions sont bien positives) on conclue que c'est convergent pour tout a,b... je sens que l'erreur vient de la division par ln|t|^b
Avec ta majoration tu peux déduire que si l'intégrale de ^b}) converge alors l'intégrale de départ converge.
converge alors l'intégrale de départ converge.
Mais tu n'as qu'une implication.
Comme on travaille avec la valeur absolue, on a affaire à des fonctions positives, donc avec les équivalents, on a... équivalence entre la convergence des intégrales des fonctions de chaque côté du symbole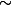 .
.
Mais tu n'as qu'une implication.
Comme on travaille avec la valeur absolue, on a affaire à des fonctions positives, donc avec les équivalents, on a... équivalence entre la convergence des intégrales des fonctions de chaque côté du symbole
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
