Intégrales généralisées

par **CC_** » 20 Sep 2006, 19:36

Bonjour! :we:
Nous venons de commencer les intégrales généralisées, j'aurais un petit service à vous demander pour un calcul tout bête.

Il s'agit

, j'ai tenté une ipp qui ne semble pas aboutir. Quelle méthode serait à employer ici?

Merci bien!

par **Alexandre_de_Prepanet** » 20 Sep 2006, 19:59

L'énoncé de l'exercice te propose quoi ? de calculer la valeur de cette intégrale ?

par **abcd22** » 20 Sep 2006, 20:02

Bonsoir !
Peut-être un changement de variable

?

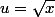
par **Alexandre_de_Prepanet** » 20 Sep 2006, 20:03

abcd22 a écrit:Bonsoir !
Peut-être un changement de variable ?

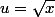
Bof... Je vois bien un petit critère de Riemann perso

par **abcd22** » 20 Sep 2006, 20:04

C'était pour calculer l'intégrale, pas pour prouver la convergence.

par **Alexandre_de_Prepanet** » 20 Sep 2006, 20:08

De toute façon, t'en que tu n'as pas prouver la convergence tu peux rien faire donc ...

par **tize** » 20 Sep 2006, 20:20

Plutot d'accord avec abcd22, ici la convergence ne pose aucun problème et avec le changement de variable

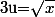
puis une IPP on trouve facilement la solution...

par **CC_** » 20 Sep 2006, 20:42

Bonjour tous les trois,

abcd22 a écrit:C'était pour calculer l'intégrale, pas pour prouver la convergence.

Ben... On fait les deux en même temps, plus ou moins, non?

Merci pour l'idée du changement de variable, ça marche! :happy2:

par **abcd22** » 20 Sep 2006, 20:55

CC_ a écrit:Ben... On fait les deux en même temps, plus ou moins, non?

Non, il faut justifier la convergence avant de faire des calculs pour trouver la valeur de l'intégrale (surtout qu'ici c'est pas compliqué).

par **CC_** » 20 Sep 2006, 21:07

Donc il faut faire une preuve à part montrant la convergence de l'intégrale? Mais comment? En trouvant une intégrale convergente qui majore celle-ci, il n'y a que ça ou d'autres méthodes?

par **abcd22** » 20 Sep 2006, 21:11

Tu n'as pas vu le critère de Riemann dont parle Alexandre ?

par **CC_** » 20 Sep 2006, 21:18

Si, mais je parlais en général en fait :we: On ne pourra pas appliquer Riemann à toutes les intégrales, et pour celles où le critère n'est pas applicable, comment est-on censé procéder pour démontrer la convergence à part?

par **CC_** » 20 Sep 2006, 21:21

Comme critère de Riemann, j'ai bien vu celui des

, mais je ne vois pas trop comment l'appliquer ici.
De toute manière, ma question avait une portée générale en fait :we: On ne pourra pas appliquer Riemann à toutes les intégrales, et pour celles où le critère n'est pas applicable, comment est-on censé procéder pour démontrer la convergence à part?

par **abcd22** » 20 Sep 2006, 21:28

Ici la fonction à intégrer est positive et en l'infini

donc on peut utiliser le critère de Riemann. Le plus souvent pour prouver l'intégrabilité on prend un équivalent (après avoir vérifié que la fonction était de signe constant), ou alors on majore par quelque chose qu'on sait calculer (pour

sur

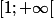
on utilise

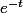
par exemple).

par **CC_** » 20 Sep 2006, 21:34

Ah d'accord! mais nous n'avons pas encore vu les équivalents (cela fera l'objet du prochain cours!).
Je te remercie pour toutes ces explications! :++:
Bonne soirée à toi!

Intégrales généralisées

Intégrales généralisées

Qui est en ligne