Intégrales généralisées

[adrien69]

Pas de soucis.

Pour la deuxième inversion, , on a comme bornes 0 et pi/2 comme les bornes de l'intégrale après la première inversion sont 0 et pi/2. Du coup, pour n impair,



Je ne vois pas comment me débarrasser du -.

Ouais t'as mal inversé tes bornes.

Quand x vaut pi/2, vaut 0. Et vice-versa.

[Vupen]

Je ne vois pas pourquoi je devrais inverser les bornes. C'est bien le plus petit en bas ? Car lorsque x vaut 0, on a theta = pi/2.

EDIT : Non ok je n'ai rien dit, c'est dans la formule de changement de variables, merci.

[Vupen]

Pour la dernière question, je suppose qu'il faut utiliser le théorème 13.20 (http://www-fourier.ujf-grenoble.fr/~rombaldi/Capes/AnalyseChap13.pdf , pg 277).

On a, comme :



Reste à montrer que la série converge, sauf qu'on ne peut pas dire grand chose, ou alors quelque chose m'a échappé.

[adrien69]

Il faut, dans un sens (si on suppose d'abord que I converge) utiliser le 13.19, et dans l'autre sens le 13.20.

Le tout est de comparer ln(f(cn))/f(cn) avec les quantités que tu as déjà (*)

Ie montrer de proche en proche que la série des ln(f(cn))/f(cn) converge ssi la série des vn converge grâce au petit 1et aut truc que tu auras fait à ma petite étoile . Et après utiliser tes deux théorèmes.

[Vupen]

Qu'entends-tout par "montrer de proche en prche" ?

[adrien69]

Tout simplement démontrer tranquillement ^^ c'était pas mathématique comme expression. Tkt.

[Vupen]

Y a un petit soucis avec le th.19. En effet, dans les hypothèses, il est stipulé "pour toute suite x_n" or dans mon exo, on particularise x_n avec n*pi/2 ... Je pense que ce théorème, par sa contraposée, s'utilise plutot pour démontrer une divergence.

[Vupen]

Mais on est d'accord, faut utiliser la double inégalité du 1. (le sens à utiliser dépendant du sens de l'équivalence que l'on démontre), je regarde ça.

[adrien69]

Nope. En fait il va falloir que tu l'utilises pour une implication (celle I converge donc), et le 20 pour (il existe une suite, je l'ai exhibée donc I converge)

Ouep t'as besoin de l'inégalité. Et bien dans un sens puis dans l'autre.

[Vupen]

Déjà, je peux remplacer par ?

[adrien69]

Euh ouais mais je vois pas l'intérêt :/

[Vupen]

Récapitulons, car je m'embrouille.





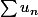
On suppose que I converge. Alors d'après le th 19, la série converge, et donc d'après (**) la série (le membre de droite) converge aussi mais ... on ne peut rien dire des séries Du coup, je ne vois pas quel(s) argument(s) utiliser :\

[adrien69]

Ben déjà il sort d'où ton ln(pi/2)/f(cn) ?

Pour faire simple :

u_n \leq v_n \leq \frac{2\ln (1+f(c_n)\frac{\pi}{2})}{f(c_n)} \sim \frac{2\ln f(c_n)}{f(c_n)}
Et donc CQFD comme on a des séries à termes positifs au bout d'un certain rang.

[Vupen]

Je me suis compliqué la vie en effet ... Bah j'avait mis en facteur f(cn)*pi/2 dans le ln puis utilisé ln(ab) = ln a + ln b ...

Encore merci.