Fonction définie par une intégrale

[ekexopa]

Bonsoir,

J'ai la fonction f définie par :

Je pense que son domaine de définition est R et qu'elle est paire.
De plus, avec le changement de variable u=1/t , j'obtiens que f(1) = - f(1) donc f(1) = 0.

A partir de là, on me demande d'en déduire une forme explicite de f, et je ne vois pas comment faire.

Une idée ?

Merci !

[AlexisD]

Je crois que le changement de variable que tu as effecuté est inutile.
Pour bien rédiger, tu dois montrer que la fonction à l'intérieur de l'intégrale est justement intégrable en 0 et à l'infini. A priori ce n'est pas simple car elle est définie sur ]0,+ [
Il faut utiliser des majorations ou des équivalents.

[Pythales]

Pour la définition aux bornes, que vaut ? A l'infini, comment majorer ?
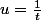
et le changement de variable te donne directement la valeur de