L1+L2=L(E) et L1,L2 commutent

[anthony2001]

Bonjour
j'aimerais bien de l'aide pour trouver les sous espaces L1,L2 de End(E) dimE fini tels que L1+L2=End(E) et pour tout f1de L1 et f2 de L2 f1of2=f2of1
question posée à l'oral de centrale en 2007
merci

[prody-G]

Hmm

Si H = {homothéties sur E}, c'est un K-espace vectoriel en tant que sous espace de End(E).
H possède un supplémentaire dans End(E) qu'on appelle G.
Puis il est clair que pour tout h dans H et pour tout g dans G, hg=gh.

La réciproque doit bien se faire par l'absurde je pense. Tu prends un matrice non scalaire et tu en exhibes une qui ne commuterait pas.

[anthony2001]

merci pour cette réponse mais la réciproque est loin d'être évidente
l'exercice n'est pas si simple c'est niveau X ,ENS sans indications
j'ai encore besoin d'aide

[yos]

question posée à l'oral de centrale en 2007

Tu es sûr de la source? c'est vrai que ça me semble pas évident.

Comme je le disais dans l'autre fil, tu peux remplacer par les sous-algèbres F,G de qu'ils engendrent. On aura encore :

, et est la droite .

A noter que pour des raisons de dimensions (Grassmann), les sev F et G obtenus ne sont guère plus gros que ceux de départ et . Au pire, on a une dimension en plus pour l'un des deux sev.

En résumé, on peut supposer que L(E) est somme directe de deux sous-algèbres qui "commutent". C'est intéressant car tout polynôme en les éléments de est dans par exemple.
contient en particulier des tas d'inversibles : pour f dans et pour presque tout .

[yos]

On doit pouvoir s'en sortir comme ça :
le commutant d'une matrice A est de dimension , les 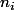étant les dimensions des sous-espaces caractéristiques (somme des 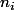= n).
Le commutant d'une matrice "individuelle" A peut donc pas être trop gros si
p>1 (i.e. A pas homothétie).
L'exo devrait en découler en prenant A "convenable" dans (le plus petit des deux sev).

[anthony2001]

merci a ceux qui ont essaye de m aider
voici des elememts de solution
a)si L1 contient f1 tel que C(f1)=K(f1) alors L2 est formes d homotheties b) puis on utilise le nilpotent d indice n f1(ei)=ei+1 puis a)