Logique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 21 Juin 2009, 18:42
par jeje56 » 21 Juin 2009, 18:42
Bonsoir,
Montrons que si x vérifie

, alors x est nul :
La logique me pose problème : utiliser la contraposée ou l'absurde ?
Supposons x non nul
alors |x|>|x|/2
d'où le résultat
OU
Supposons x non nul
Posons

donc

d'où la contradiction
Je ne comprends pas bien la deuxième méthode...
Merci bcp !
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 21 Juin 2009, 20:58
par Zavonen » 21 Juin 2009, 20:58
P(x):

Q(x): x=0
: \exist \epsilon >0 | |x|> \epsilon)
: x \neq 0)
La contraposée de
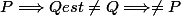
-
abdelmoaiz
- Messages: 5
- Enregistré le: 20 Juin 2009, 22:44
-
 par abdelmoaiz » 21 Juin 2009, 23:25
par abdelmoaiz » 21 Juin 2009, 23:25
Bonjour
Pour démontrer par contraposition cette proposition [TAEX]\forall |a| \leq \epsilon \Rightarrow a=0[/TEXT]
je suppose
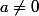
et je prends

alors

donc
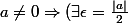 : |a|\gt \epsilon =\frac{|a|}{2})
.
aurevoir
-
abdelmoaiz
- Messages: 5
- Enregistré le: 20 Juin 2009, 22:44
-
 par abdelmoaiz » 21 Juin 2009, 23:33
par abdelmoaiz » 21 Juin 2009, 23:33
Bonjour
Pour démontrer par contraposition cette proposition [/TEX]\forall |a| \leq \epsilon \Rightarrow a=0[/TEXT]
je suppose
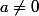
et je prends

alors

donc
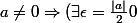 : |a|\gt \epsilon =\frac{|a|}{2})
.
et cela

a|\leq \epsilon \rightarrow a=0"/>
aurevoir
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Juin 2009, 06:54
par jeje56 » 22 Juin 2009, 06:54
Merci à toi,
Oui, j'ai donc bien montré la contraposée... Dans un livre on parle de l'absurde, mais je ne vois pas bien comment rédiger une telle démo...
Merci !
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 22 Juin 2009, 07:10
par Zavonen » 22 Juin 2009, 07:10
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Juin 2009, 07:51
par jeje56 » 22 Juin 2009, 07:51
En fait, plus précisément pour l'absurde :
La négation de A=>B est non(A=>B) donc dans notre cas on peut supposer x non nul et vérifier qu'il ne vérifie pas A... C'est bien ça ?
-
Zavonen
- Membre Relatif
- Messages: 213
- Enregistré le: 23 Nov 2006, 10:32
-
 par Zavonen » 22 Juin 2009, 09:15
par Zavonen » 22 Juin 2009, 09:15
Le raisonnement dit 'par l'absurde' consiste à supposer le contraire que ce que tu veux démontrer pour parvenir à une contradiction.
Ici il s'agit de démontrer une implication
P implique Q
Cette implication est en fait une abréviation de Q ou (non P)
La négation de Q ou (nonP) est non Q et non(nonP)
Elle est donc équivalente à non Q et P
Il faut donc que tu montres que non Q et P conduit à une contradiction.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
