Bonjour a tous
Pouvez vous m'aidez a résoudre cette équation différentielle.
Cela fait plus de 2h que je suis dessus et je m'en sors pas :briques: . HELP PLEASE!!!
(x²+y²)(1-y')²=4(y-xy')²
Merci à tous
Equation différentielle
14 messages
- Page 1 sur 1
par fatal_error » 07 Avr 2009, 18:13
salut,
je sais pas si ca peut aider, mais y=x semble etre solution
je sais pas si ca peut aider, mais y=x semble etre solution
la vie est une fête 
par mathelot » 07 Avr 2009, 18:21
Bs,
il faut déja résoudre en y', c'est la forme canonique
qui permet d'appliquer éventuellement Cauchy-Lipschtiz.
 =2 \left( y-xy' \right))
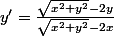
l'expression est homogène.
y est fonction de x. y=f(x).
On pose=\frac{y}{x})
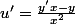
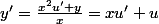
L'équation différentielle devient à variables séparées
la quantité)
étant fonction de la quantité 
Elle se résoud par une quadrature,ie,une primitive:
elle s'arrange très très bien:
une fraction rationnelle de la variable u à décomposer en éléments simples
d'un côté de l'égalité, la différentielle exacte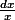
à primitiver en)
de l'autre.
je te laisse terminer :doh:
il faut déja résoudre en y', c'est la forme canonique
qui permet d'appliquer éventuellement Cauchy-Lipschtiz.
l'expression est homogène.
y est fonction de x. y=f(x).
On pose
L'équation différentielle devient à variables séparées
la quantité
Elle se résoud par une quadrature,ie,une primitive:
elle s'arrange très très bien:
une fraction rationnelle de la variable u à décomposer en éléments simples
d'un côté de l'égalité, la différentielle exacte
à primitiver en
je te laisse terminer :doh:
par gastonleretour » 07 Avr 2009, 18:58
Je te remercie beaucoup.
Je vais tenter de le refaire de mon cote avec tes explication. ( moi deja j'etais mal partie^^)
A force d'en faire j'espere que sa va rentrer :marteau:
Je vais tenter de le refaire de mon cote avec tes explication. ( moi deja j'etais mal partie^^)
A force d'en faire j'espere que sa va rentrer :marteau:
par pegase803 » 07 Avr 2009, 20:09
Bonjour
J'ai du mal a comprendre ce qui ce passe avec le u, je vois pas du tout comment on simplifie l'équation.
Merci de m'aider
J'ai du mal a comprendre ce qui ce passe avec le u, je vois pas du tout comment on simplifie l'équation.
Merci de m'aider
par mathelot » 07 Avr 2009, 20:29
re,
Les équas diff. comportent des notations spécifiques:
y au lieu de f(x).
Quand on pose
, on définit une nouvelle
fonction=\frac{f(x)}{x})
qui est dérivable comme quotient de deux fonctions dérivables.
Ensuite, si on obtient
f(u)du=g(x)dx
on dit que l'équa diff est à variables séparées.
si f et g admettent des primitives définies par des formules closes F et G,
alors dF=dG.
Si tu veux, si en chaque point x, deux fonctions ont leurs dérivées
ou différentielles égales, et si la variable appartient à un intervalle,
on peut en déduire une égalité des primitives.
ces différentielles appartiennent à un drôle d'espace:
)
h))
que l'on note
)
Les équas diff. comportent des notations spécifiques:
y au lieu de f(x).
Quand on pose
fonction
qui est dérivable comme quotient de deux fonctions dérivables.
Ensuite, si on obtient
f(u)du=g(x)dx
on dit que l'équa diff est à variables séparées.
si f et g admettent des primitives définies par des formules closes F et G,
alors dF=dG.
Si tu veux, si en chaque point x, deux fonctions ont leurs dérivées
ou différentielles égales, et si la variable appartient à un intervalle,
on peut en déduire une égalité des primitives.
ces différentielles appartiennent à un drôle d'espace:
que l'on note
par mathelot » 07 Avr 2009, 20:40
re,
dans le temps, on résolvait les équations différentielles . en cherchant des solutions exactes. (en 1930)
C'est ce que faisait par exemple georges Valiron en France avec bonheur. d'ailleurs une partie de sa thèse est encore utilisée pour l'étude de RH.
En 1900, est venu Henri Poincaré qui a développé une méthode nouvelle et moderne: étudier la dynamique des équations différentielles. En partant d'une valeur initiale, on ne résoud plus de manière exacte, on s'intéresse plutôt au comportement, à l'évolution des solutions: c'est la théorie moderne des "systèmes dynamiques"
Seulement, ton équation, elle, admet une solution exacte. On peut donc s'amuser à en exprimer la solution. c'est ce que l'on fait en posant
dans le temps, on résolvait les équations différentielles . en cherchant des solutions exactes. (en 1930)
C'est ce que faisait par exemple georges Valiron en France avec bonheur. d'ailleurs une partie de sa thèse est encore utilisée pour l'étude de RH.
En 1900, est venu Henri Poincaré qui a développé une méthode nouvelle et moderne: étudier la dynamique des équations différentielles. En partant d'une valeur initiale, on ne résoud plus de manière exacte, on s'intéresse plutôt au comportement, à l'évolution des solutions: c'est la théorie moderne des "systèmes dynamiques"
Seulement, ton équation, elle, admet une solution exacte. On peut donc s'amuser à en exprimer la solution. c'est ce que l'on fait en posant
par mathelot » 07 Avr 2009, 20:47
re,
On résoud la 1ère
 = 2 \left( y- xy' \right))
on pose
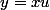
bon, tu as raison, j'ai dû me planter dans mes calculs, ça donne
plutôt:
}{\sqrt{1+u^2}-2})
}=\frac{dx}{x})
Il y a deux différentielles exactes (elles se primitivent)
Par contre, le problème , c'est de primitiver
})
on peut demander à Wolfram integrator...
ou alors alors effectuer les calculs à la main:
on pose u=sht
})
on passe à l'exponentielle, cette intégration est interminable...
on pose
dz)
On résoud la 1ère
on pose
bon, tu as raison, j'ai dû me planter dans mes calculs, ça donne
plutôt:
Il y a deux différentielles exactes (elles se primitivent)
Par contre, le problème , c'est de primitiver
on peut demander à Wolfram integrator...
ou alors alors effectuer les calculs à la main:
on pose u=sht
on passe à l'exponentielle, cette intégration est interminable...
on pose
par mathelot » 08 Avr 2009, 04:21
une primitive
avec
une courbe intégrale est donc (avec la primitive de Wolfram)
en élevant à la puissance
voili-voilou, il y a d'autres courbes intégrales
car à un moment, on a écrit que
et au tout début, on a considéré un seul facteur d'une "équation
produit nul".
Il y a un facteur
Cet exposant rend l'équation de la courbe transcendante(non algébrique).
par Pythales » 08 Avr 2009, 16:48
Le passage en polaires te tend les bras...
On trouve :
Soit
(isotropes)
soit-\rho(\sin\theta+\cos\theta+2)=0)
dont la résolution est élémentaire.
On trouve :
Soit
soit
dont la résolution est élémentaire.
par mathelot » 09 Avr 2009, 05:05
re,
je te détaille la solution de PyThales (lumineuse) :briques:
on suppose r fonction dérivable de
 \\<br />y=r sin(\theta) \\)
 - r sin(\theta) \\<br />y'=r' sin(\theta) +r cos(\theta) \\)
On peut écrire à priori localement (sans doute à cause du théorème des fonctions implicites,en fait, je ne vois pas trop mais ça s'écrit !
 +r cos(\theta)}{r' cos(\theta) - r sin(\theta)})
La 1ère équation:
=2(xy'-y))
donne
+sin(\theta)+2}{cos(\theta)-sin(\theta)})
+sin(\theta)}{cos(\theta)-sin(\theta)})
se primitive en
-sin(\theta)|))
le 2ème terme
-sin(\theta)}=\frac{\sqrt{2}}{cos(\theta+\frac{\pi}{4})})
or
}=2 \int \frac{dt}{1-t^2})
en posant)
finalement, la 1ère courbe intégrale s'exprime agréablement par:
}{1-tan(\frac{\theta}{2}+\frac{\pi}{8})} \right)^{\sqrt{2}} \left( cos(\theta)-sin(\theta) \right)^{-1})
qui s'écrit avec un argument de tangente hyperbolique:
)}}{cos(\theta+\frac{\pi}{4})})
à la TI89, les trois courbes,
celle de la 2ème équation:
=2(y-xy'))
et l'origine O (r=0)
se raccordent continuement pour n'en former qu'une seule.
je te détaille la solution de PyThales (lumineuse) :briques:
on suppose r fonction dérivable de
On peut écrire à priori localement (sans doute à cause du théorème des fonctions implicites,en fait, je ne vois pas trop mais ça s'écrit !
La 1ère équation:
donne
se primitive en
le 2ème terme
or
en posant
finalement, la 1ère courbe intégrale s'exprime agréablement par:
qui s'écrit avec un argument de tangente hyperbolique:
à la TI89, les trois courbes,
celle de la 2ème équation:
et l'origine O (r=0)
se raccordent continuement pour n'en former qu'une seule.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :