Serie harmonique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
moimickey2
- Messages: 7
- Enregistré le: 24 Jan 2009, 15:49
-
 par moimickey2 » 24 Jan 2009, 16:34
par moimickey2 » 24 Jan 2009, 16:34
Bonjour à tous,
je viens de m'inscrire au forum, aussi même si c'est un peu tard, je vous souhaite à tous une excellente année 2009.
Sinon, j'ai un petit souci, je ne me souviens plus de comment on calcule la somme de la série harmonique de terme général Un = (-1)^n/n
Je sais que le résultat est ln(2).
Si quelqu'un peut juste me rappeler le départ.
Merci d'avance et bonne journée.
Moimickey2.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 24 Jan 2009, 17:23
par Pythales » 24 Jan 2009, 17:23
Le calcul formel est facile
Partir du développement de
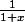
(somme de série géométrique), et intégrer terme à terme
La justification est un peu plus délicate
-
moimickey2
- Messages: 7
- Enregistré le: 24 Jan 2009, 15:49
-
 par moimickey2 » 24 Jan 2009, 18:39
par moimickey2 » 24 Jan 2009, 18:39
Merci beaucoup
Moimickey2
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 24 Jan 2009, 18:43
par Joker62 » 24 Jan 2009, 18:43
La justification se fait aisément avec le Théorème d'Abel...

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 24 Jan 2009, 19:36
par fatal_error » 24 Jan 2009, 19:36
On peut aussi la retrouver avec le developpement en serie d'hélène :
= - \sum \frac{(-x)^n}{n})
En posant

, on a alors
=\sum \frac{(-1)^n}{n})
sauf boulette
la vie est une fête

-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Jan 2009, 20:05
par ThSQ » 24 Jan 2009, 20:05
Perso je dirais plutôt -ln(2) :id:
Une façon 100% élémentaire :
^{k+1}}{k}} = \sum _{k=n+1}^{2\,n}\frac{1}{k})
puis on compare avec une intégrale
et une autre :
^{k+1}}{k}} = \sum_1^n \int_0^1 (-1)^{k}x^k dx = \ln (2) - \int _{0}^{1}\!{\frac {{x}^{n}}{1+x}}{dx})
MoiMinnie
-
moimickey2
- Messages: 7
- Enregistré le: 24 Jan 2009, 15:49
-
 par moimickey2 » 25 Jan 2009, 23:10
par moimickey2 » 25 Jan 2009, 23:10
Bonsoir,
Merci beaucoup MoiMinnie, j'aime bien la deuxième surtout que c'était le point de départ pour montrer que selon les groupements de termes, on pouvait arriver à la somme qu'on voulait.
Encore merci à tous et à bientôt sur ce forum
Moimickey2
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 26 Jan 2009, 11:13
par ThSQ » 26 Jan 2009, 11:13
moimickey2 a écrit:selon les groupements de termes, on pouvait arriver à la somme qu'on voulait.
Ex archi-classique (surtout pour un agrégatif

: Mq c'est vrai pour toute série semi-convergente.
-
moimickey2
- Messages: 7
- Enregistré le: 24 Jan 2009, 15:49
-
 par moimickey2 » 26 Jan 2009, 22:43
par moimickey2 » 26 Jan 2009, 22:43
Bonsoir,
j'avoue que je ne sais pas trop comment le prouver, mais cela semble montrable après de longues recherches... :)
Au fait quel concours passes-tu ?
Moimickey2
-
Lemniscate
- Membre Relatif
- Messages: 300
- Enregistré le: 18 Jan 2009, 19:55
-
 par Lemniscate » 26 Jan 2009, 23:45
par Lemniscate » 26 Jan 2009, 23:45
Euhh il est tard j'ai peut-être pas vu mais je crois que j'ai une autre démo très facile, dès que l'on sait que :
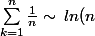)
pour
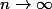
.
résultat que je démontre avec

et un passage à l'intégrale puis à la somme.
En effet
^{p}}{p}}=\displaystyle \sum_{p=1}^{n}{\frac{1}{2p}} - \displaystyle \sum_{p=0}^{n}{\frac{1}{2p+1}})
(en regroupant les termes positifs avec les termes négatifs).
et
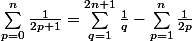
D'où
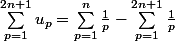
D'où :
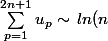-ln(2n+1))
Or
-ln(2n+1)=-[ln(\frac{2n+1}{n})]\sim\,-ln(2))
D'où le résultat !
EDIT : Je viens de voir que c'est ce que proposait en détaillant moins, ThSQ, mais bon j'ai pas envie d'effacer toutes ces belles bornes TEX !
-
moimickey2
- Messages: 7
- Enregistré le: 24 Jan 2009, 15:49
-
 par moimickey2 » 27 Jan 2009, 08:25
par moimickey2 » 27 Jan 2009, 08:25
Bonjour et merci,
j'apprécie toutes ces réponses et merci pour les détails, mais les réponses de ThSQ m'avaient permis de finir.
Merci à tous et à bientôt
Moimickey2
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 27 Jan 2009, 18:06
par ThSQ » 27 Jan 2009, 18:06
@moimickey2 : je passe le concours pour aller à la Grande Ecole
@Lemniscate : fais gaffe, soustraire des équivalents comme tu le fais est "risqué". Tu as de la chance ça marche ici mais c'est parce que \sum 1/k = cste + ln(n) + O(1/n)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
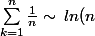) pour
pour 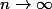 .
. et un passage à l'intégrale puis à la somme.
et un passage à l'intégrale puis à la somme.^{p}}{p}}=\displaystyle \sum_{p=1}^{n}{\frac{1}{2p}} - \displaystyle \sum_{p=0}^{n}{\frac{1}{2p+1}}) (en regroupant les termes positifs avec les termes négatifs).
(en regroupant les termes positifs avec les termes négatifs).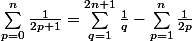
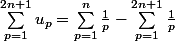
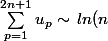-ln(2n+1))
-ln(2n+1)=-[ln(\frac{2n+1}{n})]\sim\,-ln(2))
