Série Harmonique revisitée

par **Aspx** » 06 Jan 2008, 21:40

Bonsoir!
Je suis sur un exo d'oral des Mines, j'ai trouvé quelque chose mais ça me parait trop simple pour être ça.

Le but de l'exo est de déterminer la nature de la série obtenue en enlevant les termes dont le dénominateur au moins une fois le chiffre 9 à la série harmonique.

Voilà mon raisonnement :
Une somme partielle d'une telle série serait :

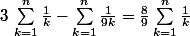
Somme partielle qui n'est pas majorée (série harmonique divergente). Donc la série reste divergente.

Merci!

par **Joker62** » 06 Jan 2008, 21:42

un naturel qui contient le chiffre 9 n'est pas forcément un multiple de 9
Et on dit une "Somme partielle"

par **Aspx** » 06 Jan 2008, 21:45

Ahh merci! J'avais pas compris dans l'écriture décimale... (c'est rectifié pour somme partielle je sais pas ce qui m'a pris).

Comment s'y prendre dans ce cas ?

par **nuage** » 06 Jan 2008, 22:50

Salut,
je ne suis pas certain de bien te comprendre.
Mais je sais que la somme des inverses des entiers ne comprenant pas le chiffre 9 dans leur écriture décimale est convergente.
Je ne souviens pas de la démonstration.
De façon heuristique, c'est assez clair : la plus part des entiers contiennent le chiffre 9 dans leur écriture décimale.

par **busard_des_roseaux** » 06 Jan 2008, 22:51

bonsoir,

un entier n de p chiffres vérifie:

soit

Ensuite, on fait du dénombrement:

Soit

le cardinal de l'ensemble des nombres de exactement p chiffres et sans 9:

les nombres de p chiffres sont obtenus en rajoutant un chiffre
différent de 0 et 9 devant un nombre de p-1 chiffres ne comprenant pas de 9.

La série amoindrie est donc convergente car majorée par la somme d'une suite géométrique convergente.

par **Aspx** » 09 Jan 2008, 14:02

Merci beaucoup busard_des_roseaux ! :++:

Série Harmonique revisitée

Série Harmonique revisitée

Qui est en ligne