[borne sup] vrai ou faux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
roror
- Messages: 7
- Enregistré le: 24 Oct 2008, 12:09
-
 par roror » 16 Jan 2009, 16:37
par roror » 16 Jan 2009, 16:37
tous est dans le titre alors vraiou faux
 \preceq \sup (a)+\sup(b))
merci
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Jan 2009, 16:39
par XENSECP » 16 Jan 2009, 16:39
Je suppose que a et b sont des fonctions car sinon le sup d'une constante ça veut rien dire :)
-
roror
- Messages: 7
- Enregistré le: 24 Oct 2008, 12:09
-
 par roror » 16 Jan 2009, 16:46
par roror » 16 Jan 2009, 16:46
a et b sont deux fonctions dans

X

-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Jan 2009, 16:51
par XENSECP » 16 Jan 2009, 16:51
Des fonctions de R dans R quoi ? Des fonctions numériques simples ? Parce que dans ce cas la réponses est FAUX.
Tu prends :
a(x)=1 et b(x)=-1-x^2
Sup(a) = 1
Sup(b) = -1
Sup(a,b) = 1
Sup(a)+Sup(b) = 0
-
roror
- Messages: 7
- Enregistré le: 24 Oct 2008, 12:09
-
 par roror » 16 Jan 2009, 16:54
par roror » 16 Jan 2009, 16:54
un exemple montrer que :
)
est une norme sur
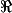
X
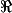
:
 = \sup( \frac{|x+ty|} {1+t^{2}}))
borne sup sur t (t est dans R)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Jan 2009, 17:02
par XENSECP » 16 Jan 2009, 17:02
Quel rapport ? Si c'était des fonctions dans R^2 bah c'est différent ^^
Enfin bref
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 16 Jan 2009, 17:12
par Doraki » 16 Jan 2009, 17:12
C'est un exemple de quoi ?
J'vois pas de fonctions a et b dans ton exemple.
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
 par R.C. » 16 Jan 2009, 17:32
par R.C. » 16 Jan 2009, 17:32
roror a écrit:un exemple montrer que :
)
est une norme sur
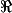
X
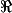
:
 = \sup( \frac{|x+ty|} {1+t^{2}}))
borne sup sur t (t est dans R)
J'ai plutot l'impression que tu cherches à voir si sup(a+b)=< sup(a) + sup(b), ce qui pour le coup est vrai.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
