Voilà, je suis Ymir, étudiant en 1ère année MPSI et notre professeur nous a donné un TD à faire pendant les vacances et à rendre par mail avant le 30 décembre... Problème, ça porte sur les polynomes et quand on a fait le cours en classe, j'ai été absent suite à une hospitalisation... Problème, malgré le fait d'avoir discuté avec lui, le prof n'a pas été compréhensif et m'a dit que le devoir valait aussi pour moi que les autres... Donc si vous pouviez m'aider à résoudre les exos ce serait sympa, merci !
[url="http://rapidshare.com/files/177877759/TD_05.pdf.html"]http://rapidshare.com/files/177877759/TD_05.pdf.html[/url]
Polynomes
11 messages
- Page 1 sur 1
par Antho07 » 29 Déc 2008, 18:08
Bonjour,
Quel exercice as-tu à faire?, qu'est-ce que tu as fais jusqu'à présent?
Quel exercice as-tu à faire?, qu'est-ce que tu as fais jusqu'à présent?
par ymir » 29 Déc 2008, 18:27
J'ai réussi à faire le 6 jusqu'à maintenant en lisant des cours en ligne mais pour le reste, je ne sais pas comment procéder -_-...
par Antho07 » 29 Déc 2008, 19:06
Dans le 7 le polynome etant réel , les racines complexes apparaissent nécesseraiment par paire de conjugués.
Donc si i est racines alors -i aussi et finalement (x²+1) divise le polynome.
Donc si i est racines alors -i aussi et finalement (x²+1) divise le polynome.
par Marie93 » 30 Déc 2008, 10:50
Pour l'exo 3 il faut que t'utilises le th : a est racine de P ssi (X-a) divise P. Sachant que X²+X+1 = ( X - j) ( X-j(barre)) tu verifies que j et jbarre est racine de ton polynome. Apres pour l'autre question c'est une simple division euclidienne.
Voila c'est ce que j'aurais fait, apres je sais pas si c'est juste ^^
Voila c'est ce que j'aurais fait, apres je sais pas si c'est juste ^^
par busard_des_roseaux » 30 Déc 2008, 11:37
Bj,
pour le (1) , les deux propriétés sont équivalentes:
i) P est divisible par^2)
ii) 1 est racine double de P
sais-tu exprimer que 1 est racine double ?
Pour le (2), le polynome diviseur a pour racines les deux racines cubiques de l'unité
et 
Il suffit d'exprimer que et 
sont racine de P,
ce qui donne par exemple que
est racine du trinôme
^m Y^2 - Y - 1)
on peut donc discuter selon m modulo 3.
pour le (3) les racines du polynôme diviseur sont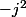
et
elles vérifient toutes les deux l'égalité
ce qui devrait aider à montrer qu'elles sont racines de P.
pour le (1) , les deux propriétés sont équivalentes:
i) P est divisible par
ii) 1 est racine double de P
sais-tu exprimer que 1 est racine double ?
Pour le (2), le polynome diviseur a pour racines les deux racines cubiques de l'unité
Il suffit d'exprimer que
ce qui donne par exemple que
on peut donc discuter selon m modulo 3.
pour le (3) les racines du polynôme diviseur sont
et
elles vérifient toutes les deux l'égalité
ce qui devrait aider à montrer qu'elles sont racines de P.
par busard_des_roseaux » 30 Déc 2008, 11:53
Pour la (4) 1 et -1 sont racines triples du polynome dérivé P'
L'ensemble des polynomes Q qui ont 1 et -1 pour racines forment un sous espace vectoriel car ils constituent l'intersection de noyaux de formes linéaires du style)
)
, etc..
Les coefficients du polynome vont donc vérifier un système linéaire
sans second membre dont la résolution donne la dimension de ce sous-espace.
Une fois résolue ces équations avec P', il suffit d'"intégrer".
pour la (5), poser la division euclidienne
)^n=(X^2+1)Q(X)+ cX + d)
en posant X= i et X= -i , un peu de calcul avec des exponentielles
complexes devrait donner les valeurs pour les inconnues c et d.
Pour la (7) voiçi quelques "idées":
i est racine. -i aussi par conjugaison. P est divisible par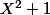
.
en développant astucieusement le carré par l'identité^2)
on factorise à vue.
sinon, P est la différence de deux carrés car
ce qui donne une factorisation en deux trinomes.
L'ensemble des polynomes Q qui ont 1 et -1 pour racines forment un sous espace vectoriel car ils constituent l'intersection de noyaux de formes linéaires du style
Les coefficients du polynome vont donc vérifier un système linéaire
sans second membre dont la résolution donne la dimension de ce sous-espace.
Une fois résolue ces équations avec P', il suffit d'"intégrer".
pour la (5), poser la division euclidienne
en posant X= i et X= -i , un peu de calcul avec des exponentielles
complexes devrait donner les valeurs pour les inconnues c et d.
Pour la (7) voiçi quelques "idées":
i est racine. -i aussi par conjugaison. P est divisible par
en développant astucieusement le carré par l'identité
on factorise à vue.
sinon, P est la différence de deux carrés car
ce qui donne une factorisation en deux trinomes.
par busard_des_roseaux » 30 Déc 2008, 12:09
Pour (7.3) on peut utiliser l'astuce bien connue
qui permet de factoriser
pour (7.3) le polynome R(X) est la somme des termes d'une progression géométrique de 1er terme le polynome 1 et de raison le monôme X.
ce qui devrait donner des idées. :we:
exercice 8: joli.
exercice 9:
)
est la partie imaginaire
de la puissance ^ k)
on peut remplacer l'indéterminée X par une racine complexe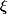
et)
par
)
sommer deux formules du binome puis résoudre des équation du 1er degré en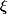
qui permet de factoriser
pour (7.3) le polynome R(X) est la somme des termes d'une progression géométrique de 1er terme le polynome 1 et de raison le monôme X.
ce qui devrait donner des idées. :we:
exercice 8: joli.
exercice 9:
de la puissance
on peut remplacer l'indéterminée X par une racine complexe
et
sommer deux formules du binome puis résoudre des équation du 1er degré en
par busard_des_roseaux » 30 Déc 2008, 12:33
exo 11 (très joli)
montrer que j est racine multiple
(regarder si P(j)=0,P'(j)=0,P''(j)=0, etc..)
comme P est à coeff réels , si j est racine disons double, aussi.
P est donc divisible par^2)
mais pépère, donc mémère :zen:
P est divisible aussi par^2)
en changeant X en -X dans l'égalité de division euclidienne.
exo 12:
Resoudre l'équation d'inconnue complexe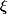
=0)
avec les racines nième de l'unité 
exo 15:
si
est racine de P et Q
et 
écrire Bezout avec m,n,d
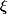est donc racine de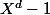 
pour la réciproque , utiliser le fait que
est divisible par 
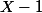si 
et donc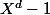 divise P et Q
montrer que j est racine multiple
(regarder si P(j)=0,P'(j)=0,P''(j)=0, etc..)
comme P est à coeff réels , si j est racine disons double,
P est donc divisible par
mais pépère, donc mémère :zen:
P est divisible aussi par
en changeant X en -X dans l'égalité de division euclidienne.
exo 12:
Resoudre l'équation d'inconnue complexe
exo 15:
si
écrire Bezout avec m,n,d
pour la réciproque , utiliser le fait que
et donc
par busard_des_roseaux » 30 Déc 2008, 13:41
exercice 13.1 calculer Ln(1). C'est chaud.
=(X^2-1)^n=(X-1)^n (X+1)^n)
utiliser la formule de dérivation d'un produit de Leibnitz:
^{(n)}=\sum_{k=0}^{k=n} \quad (_k^n) u^{(k)}v^{(n-k)})
ce qui permet d'évaluer ce polynôme dérivé n-ième en
utiliser la formule de dérivation d'un produit de Leibnitz:
ce qui permet d'évaluer ce polynôme dérivé n-ième en
par ymir » 30 Déc 2008, 23:00
Merci beaucoup ^^ ! J'ai réussi à faire la moitié des exos grâce à vous :we: !
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :