Rationnels dyadiques

[nonam]

Bonjour, j'aurais besoin d'un pti coup de main pour l'exercice suivant :

On a D = .
J'ai montré que pout tout , il existe un unique couple tel que , avec impair.
On note .
Il faut ensuite montrer que est un stathme euclidien sur D.
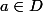
Et je bloque pour montrer que pour tout , pour tout , il existe et dans D tels que :
et ou .

Merci d'avance.

[L.A.]

Bonjour.

posons a=a'2^a'' et b = b'2^b''

je pense qu'il y a deux cas selon a''>=b'' ou non
si a''>=b'' alors on pose r le reste de a'2^(a''-b'') par b'

a'2^(a''-b'') = b'q + r puis a = bq + r2^b''

on distingue r pair ou impair pour montrer phi(r2^b'')
après... :cry:

[nonam]

edit : vais réfléchir un peu plus, parce que je crois que je dis n'imp...
en tous cas merci, ca traite deja un cas.

par contre pas besoin de distinguer r pair ou impair, si ?
On a |r|<|b'|, et (r est entier, donc divise r dans Z). Donc

[ThSQ]

Le cas phi(a) < phi(b) est clair.

Sinon on peut écrire a 2^A = q 2^Q b 2^B + r 2^R avec A = Q+B = R et a = qb+r (div euclidienne normale).

[L.A.]

par contre pas besoin de distinguer r pair ou impair, si ?

Hum... Oui finalement c'est pas la peine. Et la solution de ThSQ est meilleure.

[nonam]

yep, merci à vous deux !