Exercices sur les complexes

[sensei30]

Bonsoir bonsoir chers petits matheux! En ce moment en classe, nous abordons la notion des nombres complexes. Et j'ai là deux exercices avec lesquels j'ai un peu de mal (avec les blocus en ce moment j'ai raté deux cours de maths d'affilé =/ )

Exercice 1 :

Soient les quatre nombres complexes :
a= 2-2i b= -1+7i c= 4+2i d= -4-2i

1) réussi
2) réussi
3) Soit M le point d'affixe m=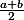
- Comparez les nombres complexes et
- Que représente la droite (MA) pour l'angle (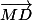,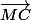) ? (ici, MD et MC sont des vecteurs)


Je trouve (sans mettre les étapes intermédiaires. Si vous pensez que j'ai tort, dites-le moi svp ^^):

m = +

= +

= +


Pour cette question, j'ai eu beau retourner les deux nombres complexes dans tous les sens, je n'arrive pas à arriver à prouver que (MA) est la bissectrice de l'angle (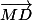,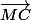), et je suis presque certaine que c'est le résultat finale à obtenir. Auriez-vous une idée de démarche ainsi que les calculs (je n'ai pas besoin de tous les détails)? J'ai d'abord tenté de comparer les arguments de ces deux complexes mais je n'arrive pas à une égalité d'angle.




Exercice 2 :
Houla, j'ai un mal dingue avec celui-ci!

A tout nombre complexe z (z 1/2), on associe le nombre complexe
Z =
On pose z = x+iy et Z = X+iY

1a) Déterminer la partie réelle X et la partie imaginaire Y de Z en fonction de x et de y.

Re(Z) = X =
Im(Z) = Y =

Je pense que c'est correct, mais bon, on n'est jamais sûr de rien!

1b) réussi (pas besoin de la réponse pour la suite de l'exercice)

2a) Montrer que si le module de z est égal à 1, alors les modules des nombres z-2 et 2z-1 sont égaux.

Ma réponse (notation du module : (module de Z)=> {Z}) :
{Z} = { (z-2)/(2z-1) } {Z} = {z-2}/{2z-1}
On pose z = 1
{Z} = {-1}/{1} = 1

D'où {Z} = 1 équivaut à {z-2} = {2z-1}


2b) Dans la suite on suppose que le module de z est égal à 1. Soient alors et ß les arguments respectifs de z et de Z.
Calculer cosß et sinß en fonction de cos;) et de sin;). Existe-t-il des valeurs de telles que z et Z aient le même argument?

Euh... Une p'tite aide? ^^

[XENSECP]

Pour le début si tu exprimais en fonction de a, b, c et d ce serait + simple ;)

[bombastus]

Bonsoir sensei30,

Pour la première, les complexes (a-m)/(d-m) et (c-m)/(a-m) sont-ils proportionnels? Comment relie-t-on les angles et les nombres complexes?

Pour l'exercice 2, je suis d'accord avec ta première réponse.

Ensuite, juste pour être sûr, c'est |z| = 1 ou |Z| = 1 que l'on suppose?

Je n'ai pas bien compris ta réponse, mais j'ai l'impression que tu utilises un cas particulier pour en déduire une expression générale...

[sensei30]

Xensecp :
Je vais tenter ça, merci du conseil!


Bombastus :
1- Je vais également prendre en compte ce conseil pour résoudre la première question.

2- C'est |z| = 1 que l'on suppose. Et en lisant ta question je me suis rendue compte que j'ai posée z=1 et pas |z|=1. En posant ça de la bonne façon, pourrais-je avoir une indication?

[XENSECP]

Lol moi j'ai rien fait ^^ Juste la flemme de réfléchir... Si tu nous avais simplement donner en fonction de a,b,c et d on aurait pu te dire tout de suite si c'était bon le résultat numérique ^^