Variable et probabilité

[sophia_d]

Bonjour je souhaiterai avoir de l'aide sur ce problème de concours qui me pose c'est le cas de le dire un problème;
On dispose de deux urnes U1 et U2 contenant chacunes deux boules identiques ne différant que par leur couleur : une blanche une noire . On prélève simultanément une boule dans chacunes de deux urnes et on les échange:On met donc dans U2 la boule prélevée dans U1 et vice versa.
Xk = nombre de boules blanches dans U1 apres la Kieme expérience
X0 = 1
1) quelle est la loi de probabilité de la variable X1 ?
2)Former le système de relation qui définit la loi de probabilité Xk eb fonction de celle de Xk-1

Pour la 1) je trouve P(X1=0)=P

Pourrais je avoir de l'aide svp merci :)

[nodgim]

On tire BB, NN, BN, ou NB (la 1ere lettre est dans U1)
X1=(1/4)*1 + (1/4)*1 + (1/4)*0 + (1/4)*2= (1/2)*1 + (1/4)*0 + (1/4)*2=1

X2= 1/2*(X1) + (1/4)*1 + (1/4)*1= 1
X3=?
Il est beaucoup plus intéressant de rechercher la probabilité d'avoir 1 boule (et une seule) dans U1!

[nuage]

Salut,
je ne comprend pas la réponse de nogidim (ou le problème).
Enfin, si j'ai bien compris le problème, en indiquant la boule sortie de U1 en premier on a 4 possibilités équiprobables :
BB ce qui donne X1=1
BN ce qui donne X1=0
NB ce qui donne X1=2
NN ce qui donne X1=1

Pour la suite il suffit de remarquer que si alors 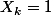avec une probabilité égale à 1.

[nodgim]

Salut,
je ne comprend pas la réponse de nogidim (ou le problème).
Enfin, si j'ai bien compris le problème, en indiquant la boule sortie de U1 en premier on a 4 possibilités équiprobables :
BB ce qui donne X1=1
BN ce qui donne X1=0
NB ce qui donne X1=2
NN ce qui donne X1=1

Pour la suite il suffit de remarquer que si alors avec une probabilité égale à 1.

C'est une question subsidiaire que je posais: Probabilité d'avoir une boule blanche, 2 boules blanches, aucune boule blanche dans U1 quand k tend vers l'infini ?

[nuage]

C'est une question subsidiaire que je posais: Probabilité d'avoir une boule blanche, 2 boules blanches, aucune boule blanche dans U1 quand k tend vers l'infini ?

Je me la suis aussi posée, et j'ai même fait le calcul : ça faisait longtemps que je n'avais plus diagonalisé de matrice.
À ma grande surprise le résultat était conforme à mon intuition.

[nodgim]

Je me la suis aussi posée, et j'ai même fait le calcul : ça faisait longtemps que je n'avais plus diagonalisé de matrice.
À ma grande surprise le résultat était conforme à mon intuition.

Mais encore ? :we:

[nuage]

[nodgim]

Ouuuuiiiiii!!! :we:

[nuage]

Ouuuuiiiiii!!! :we:

Il n'y a pas là de quoi fouetter un chat.
C'est un résultat assez trivial.