Fonctions polynomes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 30 Oct 2008, 19:23
par tybo77 » 30 Oct 2008, 19:23
Bonjour tout le monde,
je seche encore (et pour toujours ? )
Determiner un polynome P de degré 3 (avec des x cubes ?) tel que pour tout reel x, P(x+1)-P(x) = (x-1)(x+1)
devellopper ?
En deduire en fonction de n la valeur de la somme : Sn = 1*3+2*4+3*5+ ... + (n-2)n
Calculer cette somme lorsque n = 100
je pense qu'il faut remplacer n par 100 (évident) mais bon
-
aeon
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Oct 2008, 17:00
-
 par aeon » 30 Oct 2008, 19:29
par aeon » 30 Oct 2008, 19:29
1) Un polynome de degré 3 peux s'écrire sous la forme
P(x) = a*x^3 + b*x^2 + c*x + d (oui avec des x cubes)
Il faut écrire puis développer P(x+1) - P(x), puis développer (x-1)(x+1) et enfin identifier membre à membre.
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 30 Oct 2008, 19:36
par tybo77 » 30 Oct 2008, 19:36
(x+1)(ax3 + bx² + cx +d) = ax4 +bx3 +cx² +dx +ax3 +bx² +cx +d
=ax4 +bx3 + ax3 + cx² + bx² +dx +cx +d
en fait je dois prouver que
ax^4 + x^3(a+b) + x²(b+c) + x(d+c) +d = ax^4 + bx^3 + cx² +dx
ou
ax^4 + x^3(a+b) + x²(b+c) + x(d+c) +d - (ax^4 + bx^3 + cx² +dx
)=(x+1)(x-1)
-
aeon
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Oct 2008, 17:00
-
 par aeon » 30 Oct 2008, 19:50
par aeon » 30 Oct 2008, 19:50
Non, c'est pas ça.
Si P(x) = a*x^3 + b*x^2 + c*x + d, combien vaut P(x+1) ?
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 30 Oct 2008, 19:54
par tybo77 » 30 Oct 2008, 19:54
P (x+1)= ax^4 + x^3(a+b) + x²(b+c) + x(d+c) +d
ou
a(x+1)^3 + b(x+1)² + c(x+1) + d
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 10:44
par tybo77 » 31 Oct 2008, 10:44
Je remonte mon sujet au cas ou qqun pourrait m'aider
-
anthonys
- Membre Naturel
- Messages: 98
- Enregistré le: 29 Oct 2008, 09:22
-
 par anthonys » 31 Oct 2008, 10:47
par anthonys » 31 Oct 2008, 10:47
P (x+1)= ax^4 + x^3(a+b) + x²(b+c) + x(d+c) +d pas bon
ou
a(x+1)^3 + b(x+1)² + c(x+1) + d ,ça c'est mieux
Du courage, maintenant il faut développer
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 11:05
par tybo77 » 31 Oct 2008, 11:05
ca me donne
ax^3 + ax² + a2x² + a2x +ax +a +bx² +b2x +b +cx +c +d
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 11:16
par tybo77 » 31 Oct 2008, 11:16
donc :
p(x+1)= ax^3 + 3ax² +3ax +a +bx² +2bx +b +cx +c +d
ensuite p(x+1)-p(x) = 3ax² +3ax +a +2bx +b +c
que faire ensuite ? svp
-
anthonys
- Membre Naturel
- Messages: 98
- Enregistré le: 29 Oct 2008, 09:22
-
 par anthonys » 31 Oct 2008, 11:19
par anthonys » 31 Oct 2008, 11:19
ax^3 + ax² + a2x² + a2x +ax +a +bx² +b2x +b +cx +c +d
En rouge c'est pas bon!
Pour info:
^3=a^3+3a^2b+3ab^2+b^3)
-
Mirmadan
- Messages: 5
- Enregistré le: 27 Oct 2008, 17:16
-
 par Mirmadan » 31 Oct 2008, 11:21
par Mirmadan » 31 Oct 2008, 11:21
Tu dois avoir 3ax²+3ax+2bx+a+b+c=x²-1
-
Mirmadan
- Messages: 5
- Enregistré le: 27 Oct 2008, 17:16
-
 par Mirmadan » 31 Oct 2008, 11:29
par Mirmadan » 31 Oct 2008, 11:29
donc 3ax²+3ax+2bx+a+b+c=x²-1
3ax²+x(3a+2b)+a+b+c=x²-1
SSI a=1/3
3a+2b=0
c=-1
SSI a=1/3
b=-1/2
c=-1
Donc pour
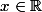
P(x)= ????? Je te laisse le faire !
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 12:26
par tybo77 » 31 Oct 2008, 12:26
je ne comprend pas bien comment tu as trouvé les inconnues a,b et c
-
Mirmadan
- Messages: 5
- Enregistré le: 27 Oct 2008, 17:16
-
 par Mirmadan » 31 Oct 2008, 12:37
par Mirmadan » 31 Oct 2008, 12:37
Pense à la définition d'une égalité de deux polynômes. ;)
Deux polynômes de même degré sont égaux SSI.... ?
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 13:01
par tybo77 » 31 Oct 2008, 13:01
Deux fonctions polynômes sont égales si et seulement si elles ont le même degré et si les coefficients des termes de même degré sont égaux.
en fait j'ai
P(x) = 1/3x^3 + 1/2x² - x (+ 0)
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 13:48
par tybo77 » 31 Oct 2008, 13:48
pour la question 2) quel est le rapport entre la somme et la premiere question (le polynome de 3ème degré) ?
-
anthonys
- Membre Naturel
- Messages: 98
- Enregistré le: 29 Oct 2008, 09:22
-
 par anthonys » 31 Oct 2008, 13:55
par anthonys » 31 Oct 2008, 13:55
A quoi est égale P(x+1)-P(x) lorsque x=n-1?
-
Mirmadan
- Messages: 5
- Enregistré le: 27 Oct 2008, 17:16
-
 par Mirmadan » 31 Oct 2008, 13:59
par Mirmadan » 31 Oct 2008, 13:59
tybo77 a écrit:Deux fonctions polynômes sont égales si et seulement si elles ont le même degré et si les coefficients des termes de même degré sont égaux.
en fait j'ai
P(x) = 1/3x^3 + 1/2x² - x (+ 0)
Voilà !

-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 14:04
par tybo77 » 31 Oct 2008, 14:04
j'ai un doute
on a
x² + 0x - 1= 3ax²+x(3a+2b)+a+b+c
a=1/3
b=-1/2
mais pourquoi on fait pas a+b+c=-1
c=-5/6
-
tybo77
- Membre Naturel
- Messages: 58
- Enregistré le: 29 Oct 2008, 17:23
-
 par tybo77 » 31 Oct 2008, 14:12
par tybo77 » 31 Oct 2008, 14:12
1/3x^3 - 1/2x² -x ou -5/6x
1/3(n-1)^3 - 1/2(n-1)² - 5/6(n-1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 179 invités
