Algèbre

[frygorn]

Bonjour à tous! J'ai un petit problème sur mon devoir et notamment sur 2 questions.
Soit f1(x)=e^x ; f2(x)=e^2x ; f3(x)=e^x² ; B=(f1,f2,f3) et E le sev engendré par la famille B .
On note G l'application qui, à f appartenant à E associe le triplet
(f(0),f '(0),f ''(0)). f ''(0) est le dérivée seconde en x=0 de f.
1)Prouvez que G est un isomorphisme de E sur R^3. ( J'ai trouvé dim E=3 mais je n'arrive pas à prouver que G est linéaire).


Ensuite on note H l'application de E dans E qui associe H(f)=Af1+Bf2+Cf3 où
A=1/4(4f(0)+2f '(0)+2f '' (0))
B=1/4(-2f(0)+f '(0)-f ''(0))
C=1/4(2f(0)-3f '(0)-f ''(0))
2)Exprimez H(f1),H(f2),H(f3) en fonction de f1,f2,f3 (H est un endomorphisme de E)
Merci d'avance.

[marie49]

Salut frygorn

Pour montrer que G est linéaire :
Soit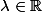 et , on a :

Et tu utilises la linéarité de la dérivée...

Après pour montrer que c'est un isomorphisme, comme tu as prouvé que dim E = 3 il suffit de montrer que ta fonction est injective.

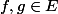signifie qu'il existe a, b, c, a', b', c' tels que :
et

Tu supposes que G(f) = G(g), et tu montres que forcément on a f=g, c'est à dire : a=a', b=b', et c=c'

[The Void]

Bonjour,

Après pour montrer que c'est un isomorphisme, comme tu as prouvé que dim E = 3 il suffit de montrer que ta fonction est injective.

f, g \in E signifie qu'il existe a, b, c, a', b', c' tels que :
f = af_1 + bf_2 + cf_3 et g = a'f_1 + b'f_2 +c'f_3

Tu supposes que G(f) = G(g), et tu montres que forcément on a f=g, c'est à dire : a=a', b=b', et c=c'

Il y a peut être plus rapide: montrer que (G(f1),G(f2),G(f3)) est libre, c'est à dire que les vecteurs ne sont pas coplanaires (déterminant non nul) ce qui assure que G est injective, donc bijective.

[frygorn]

ok merci :)

[frygorn]

Quelqu'un pourrait m'aider sur la question 2? Je trouve un résultat mais pas que en fonction de f1,f2 et f3