Sur le logarithme néperien.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 24 Jan 2008, 23:18
par tyler-durden » 24 Jan 2008, 23:18
Bonjour
le bac blanc approche, je m'exerce mais je ne comprends pas 2 équations :
comment résoudre :
ln[(x-1)/(x+2)] < (ou égal) 0
(lnx^3) = lnx
merci de me mettre sur la voie.
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 24 Jan 2008, 23:25
par rene38 » 24 Jan 2008, 23:25
Bonsoir
ln[(x-1)/(x+2)] < (ou égal) 0
Quels sont les nombres dont le logarithme est négatif ?
(lnx^3) = lnx
(ln(x))³ = ln(x) ou bien ln(x³) = ln(x) ?
-
Argentoratum
- Membre Relatif
- Messages: 231
- Enregistré le: 12 Sep 2007, 22:35
-
 par Argentoratum » 24 Jan 2008, 23:26
par Argentoratum » 24 Jan 2008, 23:26
Rappelle-toi que l'exponentielle est une fonction dérivable, continue et strictement croissante.
De plus exponentielle est la réciproque du logarithme népérien, donc
exp(ln(x)) = x.
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 24 Jan 2008, 23:30
par tyler-durden » 24 Jan 2008, 23:30
Bonsoir
rene38=> tu as raison, je me suis trompé c'est bien (ln(x))³=ln(x)
les nombres dont le logarithme est négatif ???
argentoratum => merci mais nous n'avons pas encore étudié la fonction exponentielle...
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 24 Jan 2008, 23:35
par rene38 » 24 Jan 2008, 23:35
"< (ou égal) 0" ça se dit bien "est négatif", non ?
les nombres dont le logarithme est négatif : attention, il y a 2 conditions.
(ln(x))³ = ln(x) : tout dans le même membre et tu factorises (3 solutions)
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 24 Jan 2008, 23:39
par tyler-durden » 24 Jan 2008, 23:39
(ln(x))³ = ln(x)
<=> (ln(x))³ - ln(x) = 0
<=> [(ln(x))³/ ln(x)] = 0
<=> (ln(x))^2 = 0
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 24 Jan 2008, 23:42
par rene38 » 24 Jan 2008, 23:42
(ln(x))³ = ln(x)
(ln(x))³ - ln(x) = 0
[(ln(x))³/ ln(x)] = 0 ???
Comment la soustraction se transforme-t-elle en division ?
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 24 Jan 2008, 23:45
par tyler-durden » 24 Jan 2008, 23:45
c'est a dire que j'ai suivi la formule ln(a)-ln(b) = ln(a/b)
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 24 Jan 2008, 23:51
par rene38 » 24 Jan 2008, 23:51
c'est a dire que j'ai suivi la formule ln(a)-ln(b) = ln(a/b)
Ce n'est pas ce que tu as écrit ; factorise le 1er membre et n'oublie pas les conditions d'existence (domaine de définition ? valeurs interdites ?)
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 24 Jan 2008, 23:55
par tyler-durden » 24 Jan 2008, 23:55
okey.
donc :
(ln(x))³ = ln(x)
ln(x) doit etre >0
domc D= ]0;+infini[
mais pour la factorisation, excuse moi mais je ne vois vraiment pas comment faire...
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 25 Jan 2008, 00:30
par rene38 » 25 Jan 2008, 00:30
ln(x) doit etre >0
Non, c'est x qui doit l'être.
Tu ne sais pas factoriser (ln(x))³
- ln(x) ? (ou bien a³ - a)
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 25 Jan 2008, 12:54
par tyler-durden » 25 Jan 2008, 12:54
a³ - a
<=> a(a^2-1)
donc (ln(x))³ - ln(x) =0
ln(x)[(lnx)^2-1] =0
c'est ça, non ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 25 Jan 2008, 13:10
par raito123 » 25 Jan 2008, 13:10
tyler-durden a écrit:a³ - a
a(a^2-1)
donc (ln(x))³ - ln(x) =0
ln(x)[(ln(x))^2-1] =0
c'est ça, non ?
Ouais!
tu peux encore factoriser
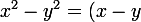(x+y))
Les multiples ne doivent pas être utilisés sans nécessité
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 25 Jan 2008, 16:40
par tyler-durden » 25 Jan 2008, 16:40
emm oui je sais mais en quoi ca m'avance :hein: ?
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 25 Jan 2008, 17:47
par rene38 » 25 Jan 2008, 17:47
tyler-durden a écrit:emm oui je sais mais en quoi ca m'avance :hein: ?
A avoir une équation-produit avec des facteurs du premier degré.
-
tyler-durden
- Membre Naturel
- Messages: 14
- Enregistré le: 19 Sep 2007, 17:25
-
 par tyler-durden » 25 Jan 2008, 22:11
par tyler-durden » 25 Jan 2008, 22:11
euh ah okey !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
