Ah d'accord :id:
merci beaucoup !
par contre dans la démonstration on met :
-f est continue sur
-f est strictement croissante sur
Mais pas sur l'intervalle ]0;5] si ?? et elle n'est pas strictement croissante ou strictement décroissante :hum:
Problèmes sur logarithme néperien
31 messages
- Page 2 sur 2 - 1, 2
Bonjour !
J'ai fini la premiere partie de l'exercice qui en fait était assez simple, je compliquait les choses :marteau:
La j'arrive à la partie économique avec une dérivée sacrément difficile je trouve. Et je ne vois même pas quelle forme prendre pour la dérivé.
Voici l'énoncé :
La fonction coût moyen Cm est définie sur ]0;5] par :
Cm(x)=}{x}) =
= 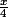 +
+ 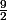
}{x})
1- Calculer Cm'(x)
Vérifier que l'on peut écrire Cm'(x) =}{2x^2}) où f est la fonction auxiliaire de la question A .
où f est la fonction auxiliaire de la question A .
Fonction auxiliaire A : f(x) =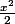 +
+ }) - 9 ln(x+1)
- 9 ln(x+1)
Merci de prendre le temps de m'aider parce que je suis vraiment perdue là !
J'ai fini la premiere partie de l'exercice qui en fait était assez simple, je compliquait les choses :marteau:
La j'arrive à la partie économique avec une dérivée sacrément difficile je trouve. Et je ne vois même pas quelle forme prendre pour la dérivé.
Voici l'énoncé :
La fonction coût moyen Cm est définie sur ]0;5] par :
Cm(x)=
1- Calculer Cm'(x)
Vérifier que l'on peut écrire Cm'(x) =
Fonction auxiliaire A : f(x) =
Merci de prendre le temps de m'aider parce que je suis vraiment perdue là !
Bonjour !
je m'y suis mise ce matin et donc j'ai commencer à faire comme pour la premiere de l'autre fois !
Soit :
Cm(x) =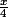 +
+ 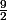 (
(}{x}) )
)
Je décompose l'équation en deux soit :
- F1(x) =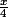
- F2(x) =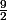 (
(}{x}) )
)
Les dérivées:
- F1'(x)= (x)(0) - (1)(4)
=
=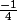
- F2(x) = (
(- (1/x+1)(x)}{x^2}) )
)
Voila ce que j'ai fait pour l'instant et le F2'(x) , je ne vois pas comment continuer apres :hum:
merci d'avance !
je m'y suis mise ce matin et donc j'ai commencer à faire comme pour la premiere de l'autre fois !
Soit :
Cm(x) =
Je décompose l'équation en deux soit :
- F1(x) =
- F2(x) =
Les dérivées:
- F1'(x)= (x)(0) - (1)(4)
=
=
- F2(x) =
Voila ce que j'ai fait pour l'instant et le F2'(x) , je ne vois pas comment continuer apres :hum:
merci d'avance !
Bonjour,
C'est presque ça.
D'une part il y a une erreur dans ton F2'. Revois la formule : u/v = (u'v-v'u)/(v²)...
D'autre part, si k est une constante, et si f est une fonction qui à x associe kx,
f'(x)=k
Du coup pour ton x/4 pas besoin de le dériver comme un quotient, en fait il s'agit de x multiplié par une constante, 1/4.
C'est presque ça.
D'une part il y a une erreur dans ton F2'. Revois la formule : u/v = (u'v-v'u)/(v²)...
D'autre part, si k est une constante, et si f est une fonction qui à x associe kx,
f'(x)=k
Du coup pour ton x/4 pas besoin de le dériver comme un quotient, en fait il s'agit de x multiplié par une constante, 1/4.
31 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
