rienbonjour, j'ai tout un exercice pour demain sur les barycentres ( enfait c'est un DM) et pour le moment je n'y arrive pas !merce de m'aider
voilà l'énoncé :
ABC est un triangle isicèle en A de hauteur [AH} tel que AH = BC = 4cm
1) construire en justifiant, le point G barycentre du système des points pondérés ( A;2) (B;1) (C;1)
( j'ai répondu à cette question et j'ai trouvé que AG = 1/4 AB + 1/4 AC soit G milieu de AB)
2a) MOntrer que vecteur V = 2MA - MB - MC est un vecteur de norme 8 . ( j'arrive pas du tout à faire le calcul même si je vois un peu le principe ! )
b) déterminer et construire l'ensemble E des points du plan tel que:
||2MA + MB + MC|| = ||V||
3) On considère les points pondérés (A;2) ( B:n) (C:n)
a) montrer que le barycentre Gn de ce système existe quelque soit la valeur de n
b)placer en justifiant G0, G1 et G2
c)Prouver que Gn appartient au segment [AH] quelque soit n .
d) soit (En) l'ensemble des points M du plan tel que :
|| 2MA +nMB +nMC|| = n||V||
démontrer que (En) est un cercle qui passe par A . Préciser son centre et son rayon.
c) calculer la distance AGn en fonction de n
4) soit la fonction f(x) = 4x / x +1
a) montrer que f(x) = 4 - (4/x+1) pour tout réel x de R \ { -1 }
b) montrer que f est positive, strictement croissante et majorée par 4 sur [0: + l'infini[
c) en utilisant le comportement de la courbe représentant f, sur la calculatrice, quand x est très très grand positif reprendre la question 3e et déduire le comportement de (EN) dans de cas .
Voilà l'exercice est très long et je m'excuse d'avance pour le temps que je vous ferai perdre mais là c'est très important !
merci
céline
DM sur les barycentres
4 messages
- Page 1 sur 1
Chère Céline !
Ce forum a été créé pour aider les gens qui veulent faire des maths et qui ont besoin d'un petit coup de pouce. Pas pour faire les devoirs des gens qui s'y prennent au dernier moment.
Tu comprends bien qu'au dernier moment, on n'a plus le temps de dialoguer pour te faire progresser pas à pas dans la solution d'un problème. On n'est pas constamment à l'écoute et un aller et retour, ça peut bien prendre 24 heures ! Donc, si tu as un gros problème à faire, tu dois t'y prendre plusieurs jours à l'avance.
Voilà pourquoi les titres genre "Urgent", "Vite" , "DM pour demain", sont proscrits ici. J'ai bien vu que tu n'avais choisi aucun de ces titres, mais il n'en reste pas moins vrai que c'est bel et bien un DM pour demain !
Ce forum a été créé pour aider les gens qui veulent faire des maths et qui ont besoin d'un petit coup de pouce. Pas pour faire les devoirs des gens qui s'y prennent au dernier moment.
Tu comprends bien qu'au dernier moment, on n'a plus le temps de dialoguer pour te faire progresser pas à pas dans la solution d'un problème. On n'est pas constamment à l'écoute et un aller et retour, ça peut bien prendre 24 heures ! Donc, si tu as un gros problème à faire, tu dois t'y prendre plusieurs jours à l'avance.
Voilà pourquoi les titres genre "Urgent", "Vite" , "DM pour demain", sont proscrits ici. J'ai bien vu que tu n'avais choisi aucun de ces titres, mais il n'en reste pas moins vrai que c'est bel et bien un DM pour demain !
1) Tu veux dire G milieu de [AH]. On peut aussi utiliser les barycentres partiels
2) Tu injectes A dans ton vecteur, et tu vois que les M s'éliminent et ton vecteur vaut
b) tu injecte G dans le premier vecteur, ton équation devient (puisque la partie
(puisque la partie  va s'éliminer)
va s'éliminer)
la réponse est donc un cercle
3) a) un barycentre existe si la somme totale des poinds n'est pas nulle. Ici combien vaut-elle ?
b) fastoche
c) encore l'associativité (ou alors tu injectes H dans
d) même méthode que pour le 2b)
e) on a dans le c) en fonction de
en fonction de 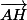
4)a) on part de la forme donnée, et on retrouve f
b) si x est positif, x+1 est supérieur à 1 donc ...
c) un peu aux autres
Une remarque : c'est très mal de se mettre à ses DM's la veille au soir, parce que si on ne trouve pas, on est mal
Quand on s'y met un peu en avance, on peut poser des questions à droite à gauche
Bonne soirée
2) Tu injectes A dans ton vecteur, et tu vois que les M s'éliminent et ton vecteur vaut
b) tu injecte G dans le premier vecteur, ton équation devient
la réponse est donc un cercle
3) a) un barycentre existe si la somme totale des poinds n'est pas nulle. Ici combien vaut-elle ?
b) fastoche
c) encore l'associativité (ou alors tu injectes H dans
d) même méthode que pour le 2b)
e) on a dans le c)
4)a) on part de la forme donnée, et on retrouve f
b) si x est positif, x+1 est supérieur à 1 donc ...
c) un peu aux autres
Une remarque : c'est très mal de se mettre à ses DM's la veille au soir, parce que si on ne trouve pas, on est mal
Quand on s'y met un peu en avance, on peut poser des questions à droite à gauche
Bonne soirée
j'ai commencé de DM depuis dimanche dernier j'avais quatre autre exos de ce genre à préparer !!!! Plus un gros DS de physique Chimie et un examen blanc de Français !! Un ami avait promis de m'aider et visiblement il m'a évité toute la semaine et ma prof était absente au cours d'aujourd'hui et personne de ma famille ne peut m'aider !
c'est sonc complètement injuste de me dire que je m'y suis pris au dernier moment ! :cry:
ps : merci galt
c'est sonc complètement injuste de me dire que je m'y suis pris au dernier moment ! :cry:
ps : merci galt
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
