Vérification de convergence d'une série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pihro
- Membre Naturel
- Messages: 16
- Enregistré le: 04 Juin 2006, 17:01
-
 par pihro » 29 Nov 2007, 15:44
par pihro » 29 Nov 2007, 15:44
Bonjour,
J'aimerai savoir si mon raisonnement est correct :
^n}{\sqrt{n}}}-1=1+\frac{1}{2}\frac{(-1)^n}{\sqrt{n}}-1+O\frac{1}{n}$)
Donc la série
^n}{\sqrt{n}}-1$)
converge.
J'ai trouvé cet exo dans un bouquin, mais ils l'ont fait autrement, alors j'aimerai savoir si ce que j'ai écrit est correct ou pas...
Merci d'avance !
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 29 Nov 2007, 16:40
par xyz1975 » 29 Nov 2007, 16:40
Bonjour,
Le DL à l'ordre 1 ne suffit pas pour en déduire la nature car on ignore la nature de la série de terme général o(1/n).
D'une manière générale la série de terme général o(Un) est covergente si la série de terme général Un est absolument convergente (il suffit de voir la définition de petit o).
NB : c'est une condition suffisante mais non nécessaire.
Un DL à l'ordre 2 s'impose ici.
-
pihro
- Membre Naturel
- Messages: 16
- Enregistré le: 04 Juin 2006, 17:01
-
 par pihro » 29 Nov 2007, 16:45
par pihro » 29 Nov 2007, 16:45
Dans le bouquin, ils ont effectivement fait un développement à l'ordre 2, mais je n'avais pas compris pourquoi il était nécessaire. C'est plus clair pour moi maintenant.
Merci et bonne fin d'après midi !
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 29 Nov 2007, 18:28
par Lierre Aeripz » 29 Nov 2007, 18:28
Il me semble que la série est divergente... Le terme en 1/n est de signe constant.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 29 Nov 2007, 18:32
par ThSQ » 29 Nov 2007, 18:32
D'accord avec "Lierre Aeripz" : c'est
^{n}/sqrt{n} \, - \, 1/n)
+ truc absolument convergent. Ca diverge
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 29 Nov 2007, 18:33
par xyz1975 » 29 Nov 2007, 18:33
Non même si le terme 1/n est de signe constant on ne peut par déduire, ils suffit d'écrire la définition de o(f). La série est convergente en faisant un DL à l'ordre 2 ce qui prouve encore une fois que ne sait pas la nature de la série de terme général o(1/n).
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 29 Nov 2007, 18:38
par Lierre Aeripz » 29 Nov 2007, 18:38
Explique toi plus... Je t'assure que la série diverge.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 29 Nov 2007, 18:43
par xyz1975 » 29 Nov 2007, 18:43
ThSQ a écrit:D'accord avec "Lierre Aeripz" : c'est
^{n}/sqrt{n} \, - \, 1/n)
+ truc absolument convergent. Ca diverge
Mais non encore une fois :
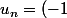^{n}/2sqrt{n} \, + \,o( 1/n))
La série de terme général
^{n}/2sqrt{n})
est convergente mais la série de terme général
)
on ne connais même pas son signe.
Rappel :
o(f) est L'ENSEMBLE de toutes les fonctions négligeable devant f
Faites un DL à l'ordre 2 vous récupérez une série convergente ?!!!!
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 29 Nov 2007, 18:49
par ThSQ » 29 Nov 2007, 18:49
Je comprends pas ce que tu dis xyz. Qui te parle de o(1/n) ????
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 29 Nov 2007, 18:55
par Lierre Aeripz » 29 Nov 2007, 18:55
Soyons plus clair...
^n}{\sqrt{n}}}-1=\frac{1}{2}\frac{(-1)^n}{\sqrt{n}}-\frac{1}{4n}+\varepsilon_n)
avec

Es-tu d'accord ?
Eh bien

est sommable, la série

converge et la série
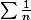
diverge. Donc la série de terme général la somme de ce trois termes diverge.
Effectivement, si on met un o(1/n) (petit 'o') plutôt qu'un O(1/n^2) (grand 'O'), on ne peut pas conclure.
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 29 Nov 2007, 18:57
par klevia » 29 Nov 2007, 18:57
Bonsoir à tous,
Pour montrer que la serie
^n}{\sqrt {n}}}-1)
converge , il suffit de multiplier par l'expression conjugué.
Au numérateur, il reste
^n}{\sqrt n})
et au denomiteur quelque chose de borné et plus grand que 1
Précisement, on obtient ceci:
^n}{\sqrt n}}{ {\sqrt{1 + \frac {(-1)^n}{\sqrt {n}}}+1})
Ainsi on obtient :
^n}{\sqrt n}\le\frac {\frac {(-1)^n}{\sqrt n}}{ {\sqrt{1 + \frac {(-1)^n}{\sqrt {n}}}+1}}\le \frac {(-1)^n}{3\sqrt n})
D'ou d'après le critère des serie alterné, la série converge
J'espère ne pas avoir dit de bétise ...
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 29 Nov 2007, 19:04
par xyz1975 » 29 Nov 2007, 19:04
Je suis d'accord avec vous, j'ai pas vérifié les calculs mais j'ai répondu à pihro par rapport à la série o(1/n).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
+ truc absolument convergent. Ca diverge