Equation différentielle

par **Nightmare** » 29 Oct 2007, 01:04

Bonsoir à tous :happy3:

Je voudrais proposer un petit exercice pour mettre en évidence un phénomène sur les équadiffs souvent oubliés par les étudiants (bien sûr les habitués n'auront pas de mal à trouver la faille).

Résoudre sur

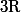
l'équation différentielle

A vos claviers.

:happy3:

par **mehdi-128** » 29 Oct 2007, 01:08

Nightmare a écrit:Bonsoir à tous :happy3:

Je voudrais proposer un petit exercice pour mettre en évidence un phénomène sur les équadiffs souvent oubliés par les étudiants (bien sûr les habitués n'auront pas de mal à trouver la faille).

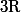
Résoudre sur l'équation différentielle

A vos claviers.

:happy3:

Bonsoir
La solution sans second membre est après calcul:si on enlève le cas x=0:

alpha.[exp(-x/2) /sqrt(x) ]

par **Nightmare** » 29 Oct 2007, 01:12

Ca ne répond pas à la question...

Je demande les solutions sur R et tu me donnes les solutions de l'équation sans second membre et pour x=0, il y a comme un problème...

par **mehdi-128** » 29 Oct 2007, 01:32

Nightmare a écrit:Ca ne répond pas à la question...

Je demande les solutions sur R et tu me donnes les solutions de l'équation sans second membre et pour x=0, il y a comme un problème...

Exact il me semble qu'il y a 2 cas :

Sur I=]-inf,0[ on prend alpha 1.

Sur J=]0,+inf[ on prend alpha 2.

suivant les 2 cas c'est la constante alpha qui change ....

par **Nightmare** » 29 Oct 2007, 01:43

J'attends de voir tes solutions finales de l'équadiff.

par **mehdi-128** » 29 Oct 2007, 01:54

Nightmare a écrit:J'attends de voir tes solutions finales de l'équadiff.

Ok je vais chercher la solution particulière qui me paraît pas évidente ...... :marteau:

par **izamane95** » 29 Oct 2007, 10:20

il faut faire la resolution deux fois une fois sur

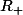
* et une fois sur

*
d'abord sur

*
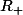
je trouve comme solution de l'equation homogène

la solution particulière est de la forme

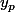
(x)=

je trouve

mais j'arrive pas a trouver une primitive de ça là ...!!!

par **namfoodle sheppen** » 29 Oct 2007, 11:13

ce que je comprends pas c'est que y et y' sont définis sur R y aura toujours un problème en -1 non ?

par **namfoodle sheppen** » 29 Oct 2007, 11:15

oublie ce que j'ai dis si faut trouver les intervalles de définitions de l'équation :id:

par **tize** » 29 Oct 2007, 11:30

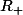
izamane95 a écrit:il faut faire la resolution deux fois une fois sur * et une fois sur *
d'abord sur *
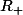
je trouve comme solution de l'equation homogène
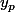
la solution particulière est de la forme (x)=

je trouve mais j'arrive pas a trouver une primitive de ça là ...!!!

Bonjour,
je ne sais pas comment tu as fait, moi j'ai trouvé comme solution de l'équation homogène :

. Il y a évidement un problème en 0 ce qui veut dire que l'ensemble des solutions sur

tout entier n'est pas un e.a. de dimension 1; ceci n'empêche pas l'existence de solutions particulières sur

tout entier...
Une solution sur

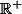
est

prolongeable par 1 en 0.
J'ai la flemme de regarder si on obtient une solution sur

entier avec des valeurs absolues sous les racines...

par **alben** » 29 Oct 2007, 11:41

Bonjour,
D'accord avec Tize, sauf qu'en pronlongeant par continuité en 0, on n'a plus de constante.
Pour x<0 et différent de -1, on a une solution du genre

avec une discontinuité en 0
PS Bravo Nightmare, tu as trouvé un cas digne de ton pseudo :we:

par **Nightmare** » 29 Oct 2007, 13:04

Salut à tous :happy3:

Je vois que vous avez tous "subit" le problème du prolongement.

En effet une solution d'une équation différentielle doit non seulement être continue mais en plus dérivable partout.

En l'occurence, cette équation différentielle n'admet aucune solution puisqu'elle n'admet aucune solution dérivable sur R. Après elle admet par exemple des solutions sur certains connexes, solutions assez horribles mais que vous avez réussis à expliciter :lol3:

Bravo à tous.

:happy3:

Equation différentielle

Equation différentielle

Qui est en ligne