Relation composée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mat087
- Messages: 4
- Enregistré le: 19 Oct 2006, 17:13
-
 par mat087 » 24 Oct 2007, 00:39
par mat087 » 24 Oct 2007, 00:39
Bonjour à tous!
Voici l'exercice que j'ai à faire:
Si la relation R sur X est transitive, démontrez que la relation R  R l'est aussi.
R l'est aussi.Posons:
 \in R \wedge (y,z) \in R \Rightarrow (x,z) \in R)
 \in R \circ R \wedge (y,z) \in R \circ R \Rightarrow (x,z) \in R \circ \R)
Je dois prouver
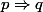
Je ne sais pas trop comment m'y prendre. Par contre, je suis presque sûr que

et
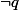
vont m'être utile.
 \in R \wedge (y,z) \in R \wedge (x,z) \notin R)
 \in R \wedge (y_1,y) \in R \wedge (y,y_2) \in R \wedge (y_2,z) \in R \wedge [ (x,y_3) \notin R \vee (y_3,z) \notin R])
Une fois cela trouvé, je n'ai aucune idée quoi faire pour faire la preuve. Auriez-vous une piste à me suggérer?
Merci,
Mathieu
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Oct 2007, 11:50
par yos » 24 Oct 2007, 11:50
Bonjour.
Comment définis-tu RoR ?
-
mat087
- Messages: 4
- Enregistré le: 19 Oct 2006, 17:13
-
 par mat087 » 24 Oct 2007, 13:41
par mat087 » 24 Oct 2007, 13:41
Que veux-tu dire par définition ?
Veux-tu dire quelque chose comme ça
 \in R \Leftrightarrow x \leq y)
, par exemple ? Si oui, je dirais dans ce cas que R n'est pas défini. Puisque, d'après moi, il faut seulement jouer avec la propriété de transitivité ici. Si non, est-ce quelque chose que je dois moi-même définir ?
Par ailleurs, j'ai trouvé ce théorème : « Une relation R sur X est transitive si et seulement

. Pourrait-il m'être utile ?
Merci,
Mathieu
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Oct 2007, 14:01
par Flodelarab » 24 Oct 2007, 14:01
C'est gênant. Cela signifie que tu ne comprends pas ce que tu cherches.
o est la loi de
composition :
Si
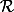
est une relation de E dans F et
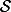
de F dans G, on peut définir une relation

de E dans G par :
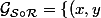 \in E \times G \, | \, \exists z \in F /\, ( x , z ) \in R \quad et \quad ( z , y ) \in S \right\} \,)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Oct 2007, 15:42
par yos » 24 Oct 2007, 15:42
Dans ce cas, il n'y a qu'à l'écrire : on prend (x,y) et (y,z) dans RoR. Puisque R est transitive, on a (x,y) et (y,z) dans R, donc (x,z) dans RoR.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 24 Oct 2007, 15:54
par Flodelarab » 24 Oct 2007, 15:54
yos a écrit:Dans ce cas, il n'y a qu'à l'écrire : on prend (x,y) et (y,z) dans RoR. Puisque R est transitive, on a (x,y) et (y,z) dans R, donc (x,z) dans RoR.
Euh ..... c'est pas si direct que ça. Il me semble qu'il faut 5 variables.
x y z d'accord
mais aussi v et w tels que xRv et vRy et yRw et wRz
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Oct 2007, 19:38
par yos » 24 Oct 2007, 19:38
Flodelarab a écrit:Euh ..... c'est pas si direct que ça. Il me semble qu'il faut 5 variables.
x y z d'accord
mais aussi v et w tels que xRv et vRy et yRw et wRz
Non. R transitive donc RoR inclus dans R.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
