Nature d'intégrales généralisées

[jamily]

Bonjour,

Soit l'intégrale d'une certaine fonction f entre 0 et +oo par exemple (avec un problème en +oo).
Je ne parvient pas à comprendre pourquoi le fait que f tende vers l'infini en +oo ne suffit pas pour affirmer que cette intégrale diverge...

Je sèche également depuis une bonne demie-heure sur la nature de :



Merci d'avance !

PS : Si quelqu'un a une méthode révolutionnaire pour résoudre les intégrales généralisées, je suis preneur...

[SimonB]

Soit l'intégrale d'une certaine fonction f entre 0 et +oo par exemple (avec un problème en +oo).
Je ne parvient pas à comprendre pourquoi le fait que f tende vers l'infini en +oo ne suffit pas pour affirmer que cette intégrale diverge....

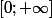
Sauf erreur de ma part, si une fonction admet une limite en l'infini et qu'elle est intégrable sur , alors sa limite est nulle.

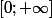
En revanche il peut y avoir des fonctions intégrables sur sans limite en l'infini (il suffit de prendre une fonction nulle presque partout et qui fait des pics autour des points entiers, de manière par exemple à ce que les pics définissent chaque fois une aire égale à 1/n² où n est l'entier considéré : cela se ramène alors à l'étude de la série de terme général 1/n²).


(Note : je parlais bien évidemment ici des fonctions à valeurs positives.)

[jamily]

Sauf erreur de ma part, si une fonction admet une limite en l'infini et qu'elle est intégrable sur [0;+\infty], alors sa limite est nulle.

Je vais peut-être dire une énorme bétise, mais si une fonction est intégrable, il n'y a pas lieu de parler d'intégrale généralisée si ?(L'intégrale serait donc convergente dans ce cas...).

En revanche, si elle n'est pas intégrable et qu'elle tend vers, comment l'aire sous la courbe pourrait-elle ne pas tendre vers ?

[SimonB]

Je vais peut-être dire une énorme bétise, mais si une fonction est intégrable, il n'y a pas lieu de parler d'intégrale généralisée si ?(L'intégrale serait donc convergente dans ce cas...).

J'ai l'impression que c'est vraiment le truc classique dans la théorie de l'intégration : tout le monde a peur de dire des énormes bêtises
On parle bien d'intégration au sens de Lebesgue, ici ?

En revanche, si elle n'est pas intégrable et qu'elle tend vers, comment l'aire sous la courbe pourrait-elle ne pas tendre vers ?

Ca, je crois vraiment que c'est impossible.

[abcd22]

Bonjour,

Je sèche également depuis une bonne demie-heure sur la nature de :

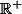
La fonction est posistive sur , à quoi est-elle équivalente au voisinage de 0 ?

[jamily]

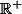
La fonction est posistive sur , à quoi est-elle équivalente au voisinage de 0 ?

Avec le développement limité de rang 1 en 0 d'une fonction composée, on obtient :

~

Cependant, si on fait , on ne trouve pas un réel non nul mais 0 !
Ce n'est dont pas un équivalent, et je suis à cours d'inspiration...

[abcd22]

Si c'est un équivalent, , la limite en 0 est l'inverse de la dérivée en 0 de , c'est-à-dire 1.

[jamily]

Je te remercie beaucoup, j'ai du faire la même bête erreur de calcul plusieurs fois de suite...